Integralberäkning

Vad skulle integralen $\int \dfrac{1}{x^2}dx$ ha för integral?

woozah skrev:

Vad skulle integralen $\int \dfrac{1}{x^2}dx$ ha för integral?

${\int }_1^2\frac{1}{x^2}dx={\left[-\frac{1}{x}\right]}_1^2$

Men är det så enkelt att jag kan se (2x+3)^2 som x^2 ? 

*Prova, derivera ditt svar och se om du får tillbaka din ursprungsfunktion, justera, upprepa från * tills det stämmer!

Smaragdalena skrev:

*Prova, derivera ditt svar och se om du får tillbaka din ursprungsfunktion, justera, upprepa från * tills det stämmer!

Vet inte hur jag ska få till det, tycker man borde kunna använda kedjeregeln, men får inte till det. Gör jag fel eller är jag ute på fel spår ? 

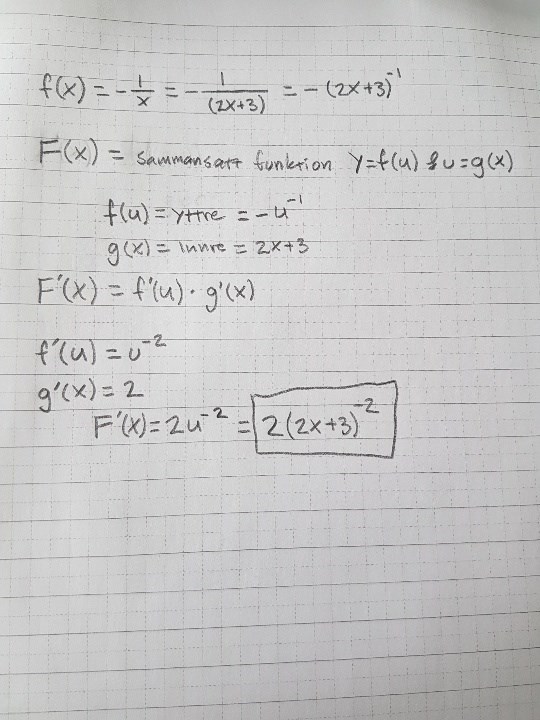
poijjan skrev:

Smaragdalena skrev:

*Prova, derivera ditt svar och se om du får tillbaka din ursprungsfunktion, justera, upprepa från * tills det stämmer!

Vet inte hur jag ska få till det, tycker man borde kunna använda kedjeregeln, men får inte till det. Gör jag fel eller är jag ute på fel spår ? 

Du krånglar till det i onödan.

Enklast och snabbast här är att bara iterera sig fram till rätt primitiv funktion.

Sätt $f(x)=(2x+3)^{-2}$.

Du letar efter en primitiv funktion $F(x)$ som är sådan att $F'(x)=f(x)$.

Du vill alltså ha en funktion som är sådan att dess derivata blir 1/(någonting)^2.

Då borde funktionen vara något liknande -1/(någonting).

--------

Första gissningen är därför att $F(x)=-(2x+3)^{-1}$.

Derivera nu $F(x)$ och jämför med $f(x)$.

Vad är det som skiljer? Är det bara en konstant faktor?

Då kan du gissa en ny $F(x)$ där du tar hänsyn till denna faktor.

Derivera din nya $F(x)$ och jämför.

Repeat until success!