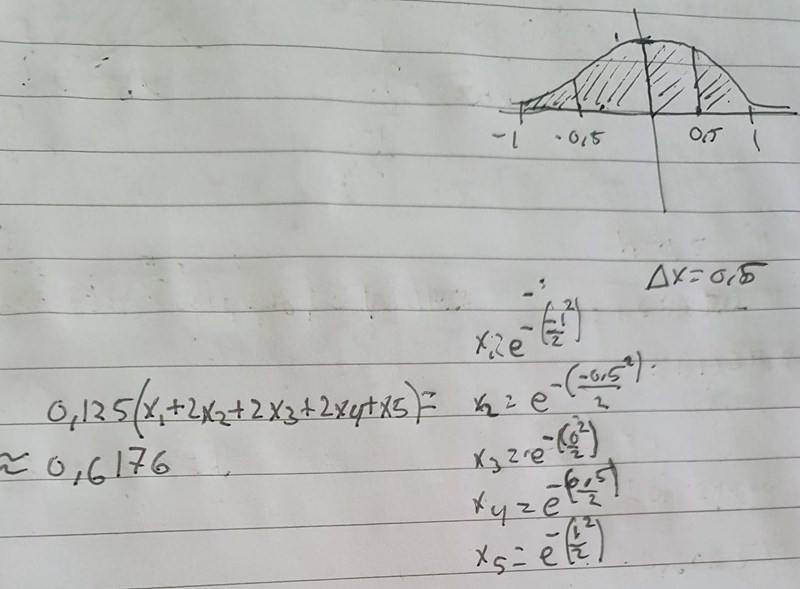Integraler -oändligheten med trapetsmetoden.
Hejsan hoppsan.
Sitter nu här igen och är lite osäker på om jag ens tänker rätt med denna uppgift,
Frågan lyder: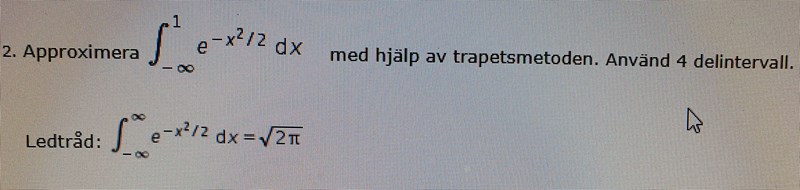
och så här har jag börjat klura: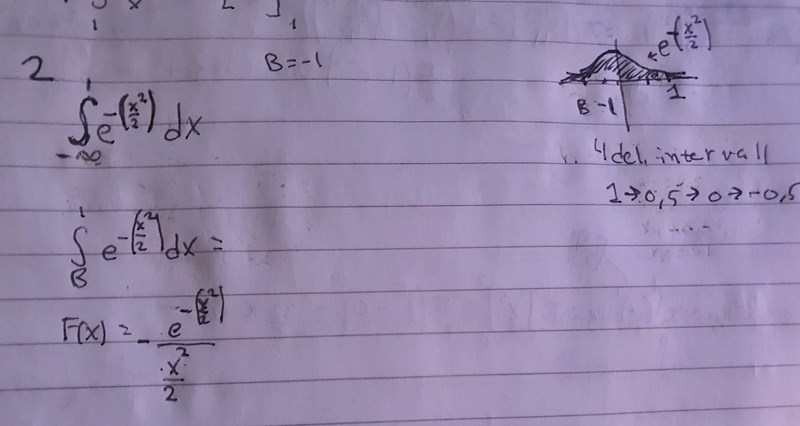
Har ersatt -Oändligheten med B och satt den på x=-1 för att kunna få ut 4 delintervaller; För att sedan använda trappetsmetoden. eller är det smidigare att sätta B till x=0 får man göra så? samt är F(x) bestämt korrekt?
Sedan borde jag då få en approximation som gäller när B->-Oändligheten?
Eller kan det vara så att jag är helt ute och cyklar...
Mvh
Den primitiva funktionen stämmer inte. Prova att derivera den får du se.
Den här funktionen har ingen elementärt uttryckbar primitiv funktion.
Det blir problem om du använder trapetsmetoden på ett oändligt långt intervall. Du har f(-0,5) i ena ändan, och 0 i andra ändan, och arean för den trapetsen (triangeln) är oändlig.
Men det är meningen att du ska använda tipset.
Jag har lite svårt att förstå hur jag ska utnyttja tipset om jag ska vara ärlig,
Ska jag välja ut ett område mellan x=1 och t.ex. x=-1, dela upp dem i 4 delintervall och få fram en approximation med täthetsfunktionen? står helt still i tänket.
NikkeB94 skrev:Jag har lite svårt att förstå hur jag ska utnyttja tipset om jag ska vara ärlig,
Ska jag välja ut ett område mellan x=1 och t.ex. x=-1, dela upp dem i 4 delintervall och få fram en approximation med täthetsfunktionen? står helt still i tänket.
Ja, börja med att beräkna integralens värde från -1 till 1 med trapetsmetoden. Eller från 0 till 1, om du vill.
Kan du avgöra värdet på integralen från till 0 med tipset?
Ja, börja med att beräkna integralens värde från -1 till 1 med trapetsmetoden. Eller från 0 till 1, om du vill.
Kan detta stämma?
"Kan du avgöra värdet på integralen från -∞-\infty till 0 med tipset? "
Nej, det skulle vara väldigt vågat av mig att påstå att jag kan..
Just för att"−∞" gör mig väldigt förvirrad..
Tips: Funktionen är symmetrisk. Hur stor är arean till höger om y-axeln jämfört med arean till vänster om y-axeln?
Smaragdalena skrev:Tips: Funktionen är symmetrisk. Hur stor är arean till höger om y-axeln jämfört med arean till vänster om y-axeln?
Exakt lika stor
Då vet du alltså arean från minus oändligheten till 0, eller hur?
Smaragdalena skrev:Då vet du alltså arean från minus oändligheten till 0, eller hur?
0,5? om totala/100% av arean är 1?
EDIT: eller
Ursäkta dubbelpost!
kan detta stämma? just för att jag använde mig av x=-1>x=1 vid trappetsmetoden. så delar bort den delen som skulle ha varit till vänster om y-axeln
Nu ser tankegången rätt ut, men jag får inte samma värde som du på resultatet av trapetsberäkningen.
Tack så hjärtligt för hjälpen!
Satt som ett stort frågetecken med uppgiften innan :)