Integraler och vänster/högerkant

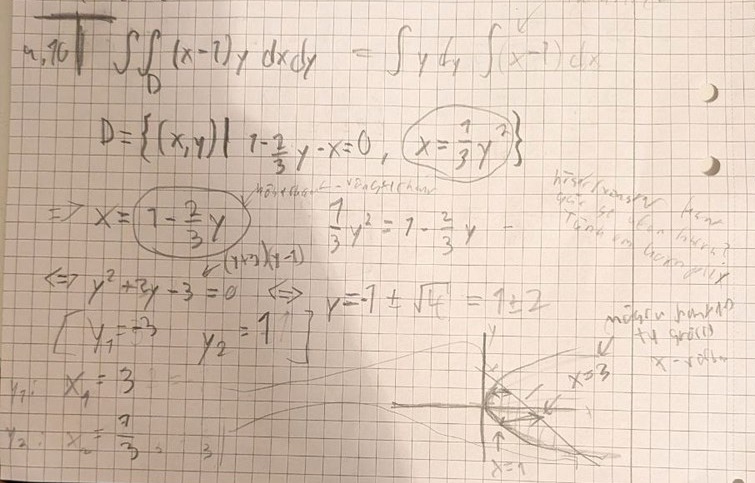
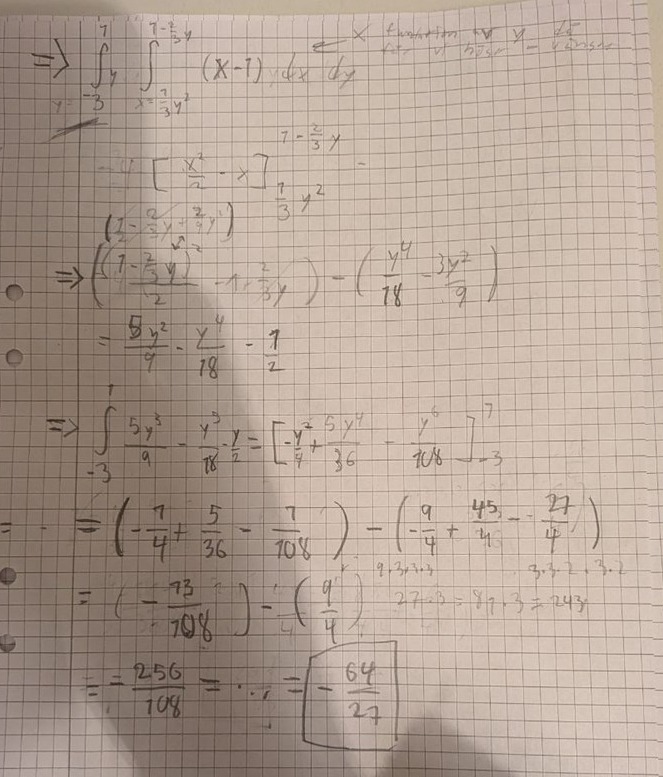
Många frågor på en gång. 

Det tråkiga svaret är: Du kan göra hur du vill, bara så länge det är rätt. Du kan dela upp det i delområden, integrera vertikalt eller horisontellt. Det finns inte en väg, det finns olika vägar.

Men ditt svar verkar vara rätt, så du har gjort rätt, på något sätt iaf.

:((((

Jag vill att det ska vara mer konkret lmao! 

Asså jag gillar att det finns alternativ men det är också dåligt på ett sätt för då måste man hålla koll på alla 75000 alternativ/verktyg lol.

Sykey skrev:

:((((

Jag vill att det ska vara mer konkret lmao! 

Asså jag gillar att det finns alternativ men det är också dåligt på ett sätt för då måste man hålla koll på alla 75000 alternativ/verktyg lol.

Dubbelintegraler följer ett par "mönster"

1. Rakt på. Yttre i x-led, inre i y-led

2. Lite mera kluriga - man vänder på den "vanliga" ordningen och har yttre i y-led och inre i x-ld

3. 2-dim variabel-byte. Brukar anges som ledning eller om det är 4 räta linjer som spänner upp en parallellogram. 

4. Polära koordinater. Finner du "x^2+y^2" i uttrycket kan du misstänka detta.

Ofta blir det inte svårare än så (men det räcker för många i början). Lös 20 av varje och du har sett det mesta - det finns inte så stor variation. 

Ibland kan områdena och uttrycken svara svåra att överblicka - då kan man ana att integranden är udda och området är symmetriskt och allt blir 0... Ett klassiskt trick.

I ett fåtal fall kan man återfå samma integral igen med någon faktor och får på så sätt en integralekvation, men det händer inte så ofta, iaf inte på för "godkänt-poäng" skulle jag tro.

Mhm... aa den med parallellogrammet har jag stött på faktiskt... det svåra med dem (för mig) är att bestämma gränserna, för oftast får man bara linjerna. 

Aa det där med udda/jämn och symmetri och sånt... asså sånt där fattar jag inte riktigt... är det sånt man måste rita upp funktionen för att se eller räcker det med denna

f(x)=f(-x)  jämn

f(-x)=-f(x) udda 

Eller lär man bara snappa upp sånt ju mer man gör? My goodness det kanske verkar självklart när jag skriver det men åndå hehe.

Sykey skrev:

Mhm... aa den med parallellogrammet har jag stött på faktiskt... det svåra med dem (för mig) är att bestämma gränserna, för oftast får man bara linjerna. 

Aa det där med udda/jämn och symmetri och sånt... asså sånt där fattar jag inte riktigt... är det sånt man måste rita upp funktionen för att se eller räcker det med denna

f(x)=f(-x)  jämn

f(-x)=-f(x) udda 

Eller lär man bara snappa upp sånt ju mer man gör? My goodness det kanske verkar självklart när jag skriver det men åndå hehe.

Tag t.ex. integralen av xy på halvcirkelskivan {x^2+y^2=r^2, y≥0} (radien spelar ingen roll). Vad kan du säga om integralens värde?

ahh that's a trick question för den säger inget om x-värdet! 

Sykey skrev:

ahh that's a trick question för den säger inget om x-värdet! 

Nja, x är väldefinierat genom området, så även y, men om vi tar t.ex. punkten (1,1) (som ger "bidraget" 1*1 till Riemannsumman) så finns även punkten (-1,1) som ger bidraget = ? - och vad blir det om man summerar dessa?

Jfr med integralen

INT_{-R}^{R} x dx

där R>0. Du behöver inte räkna ut den. Du kan säga direkt vad den är.

Bidraget blir -1, summan 0?

Oo you mf...

den andra blir också 0... mhm... detta är nytt för mig så det känns lite konstigt men okej.

Men vet inte riktigt vad du menar med att den bidrar till Riemannsumman samt så fattar jag inte hur du kan ta punkten (1,1) eller (-1,1), de är ju båda utanför enhetscirkeln? Eller kör vi bara en annan funktion helt nu lol... eller nej vänta då är ju radien $\sqrt{2}$, men det spelade ju ingen roll. Men det du ville att jag skulle säga om integralens värde för cirkeln är (antar jag) att den är 0? Det känns konstigt om det är svaret eftersom det finns ju uppenbarligen en area men jag antar eftersom att den är centrerad så finns det vissa delar som hamnar på negativa axlar?

Bäckdahls dugga? 😅

ingenjören skrev:

Bäckdahls dugga? 😅

*Uhum*... 

Här kan du se hur xy ser ut för 1:a och 2:a kvadranten.

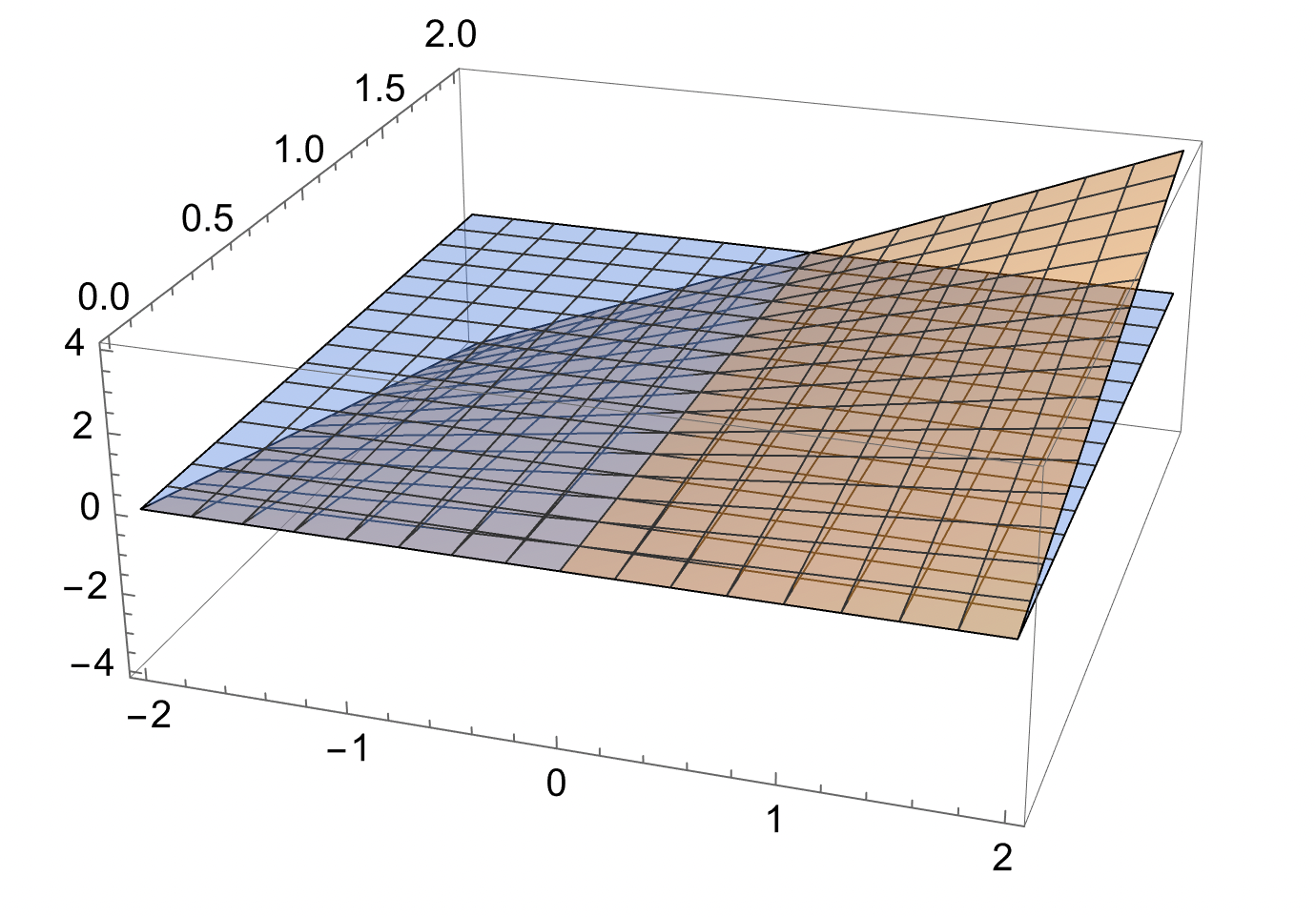
Notera att den är "lika mycket plus" som "minus". För varje positivt värde finns ett tillhörande negativt värde, varför allt summerar till 0.

Det handlar om att kunna känna igen områden och integrander. Det är alltid någon som tycker att denna typ av uppgifter är trevliga att ha på prov.

Trinity2 skrev:

Här kan du se hur xy ser ut för 1:a och 2:a kvadranten.

Notera att den är "lika mycket plus" som "minus". För varje positivt värde finns ett tillhörande negativt värde, varför allt summerar till 0.

Det handlar om att kunna känna igen områden och integrander. Det är alltid någon som tycker att denna typ av uppgifter är trevliga att ha på prov.

Hmm intressant att det blir ett plan... antar väl att dubbelintegraler kan ange antingen areor eller volymer. Det får mig att tänka på varför man egentligen har trippelintegraler... min enda teori till det är för att det finns tre variabler (that's it), venne vad skillnaden mellan dubbel/trippelintegral är annars.

Trippelintegraler kan man använda exempelvis när det finns ett skalärfält man vill integrera över. Ett enkelt exempel är att om (mass)densiteten över ett tredimensionellt område $\mathcal{H}$ ges av $\rho=\rho(x,y,z)$, ges massan av området av:

$\displaystyle m\left(\mathcal{H}\right)=\iiint_\mathcal{H}\rho\left(x,y,z\right)dV$

Det finns många andra tillämpningar också.

naytte skrev:

Trippelintegraler kan man använda exempelvis när det finns ett skalärfält man vill integrera över. Ett enkelt exempel är att om (mass)densiteten över ett tredimensionellt område $\mathcal{H}$ ges av $\rho=\rho(x,y,z)$, ges massan av området av:

$\displaystyle m\left(\mathcal{H}\right)=\iiint_\mathcal{H}\rho\left(x,y,z\right)dV$

Det finns många andra tillämpningar också.

Hur vet man om det är ett skalärfält man integrerar över? 

Ahh... coolt så man kan pinpointa vad massan är för hela objektet då?

Skalärfält är bara ett fint ord för "en funktion som tillskriver varje punkt i rummet en skalär". Anledningen till att man kallar det för det är att det också finns vektorfält som tillskriver varje punkt i rummet en vektor.

Ahh vänta är det skalärfält för att varken densitet eller massa har riktning? Det MÅSTE alltså vara ett skalärfält för dem? 

En densitet är ju bara ett tal (en skalär) och då är det per definition ett skalärfält. 

Hmm får se om jag hittar några sådana uppgifter där massan ingår såg något liknande på föreläsningsanteckningar (dessutom så förekommer det här i mekanik 1 statik då man ska hitta var masscentrum är lokaliserad). Påminner mig lite om det. 

Edit: Hittade det

Kul exempel!

Jag har en tråd från 2023 om det du kan kolla in om du är intresserad:

https://www.pluggakuten.se/trad/vad-exakt-ar-en-tyngdpunkt/

Fy vad fort tiden går...

mhm tiden går fort när man har kul ;)

Edit: Ah coolt, ska checka in på den senare idag! Lite sent just nu.

Ja, tiden rinner iväg...!

Det är faktiskt helt sjukt hur fort den går. När man var liten kändes enstaka veckor som oceaner av tid och nu, vid bara 21 års ålder, går veckor på vad som känns som ögonblick. Dessutom är nostalgin outhärdlig. Man undrar ju hur livet kommer bli när man är typ 60 när man redan nu halvt dör av nostalgi!

naytte skrev:

Ja, tiden rinner iväg...!

Det är faktiskt helt sjukt hur fort den går. När man var liten kändes enstaka veckor som oceaner av tid och nu, vid bara 21 års ålder, går veckor på vad som känns som ögonblick. Dessutom är nostalgin outhärdlig. Man undrar ju hur livet kommer bli när man är typ 60 när man redan nu halvt dör av nostalgi!

Aa vet vad du menar! Man vet inte vart tåget tänker stanna men för stunden så kör den på för fullt. 

Men jag vet vad det blir för mig... McDonalds 

Vi har tur om vi hamnar ens där med tanke på hur arbetsmarknaden ser ut... ;)

naytte skrev:

Vi har tur om vi hamnar ens där med tanke på hur arbetsmarknaden ser ut... ;)

svär... måste ha erfarhenhet... CV och förmodligen snart utbildning för att ens få kolla på byggnaden

Japp.

Hoppas du fick lite insikt i vad man kan använda trippelintegraler till, i alla fall. Nu är det dags att slagga för min del.

God natt!

Ja, samma.

God natt!