Derivata

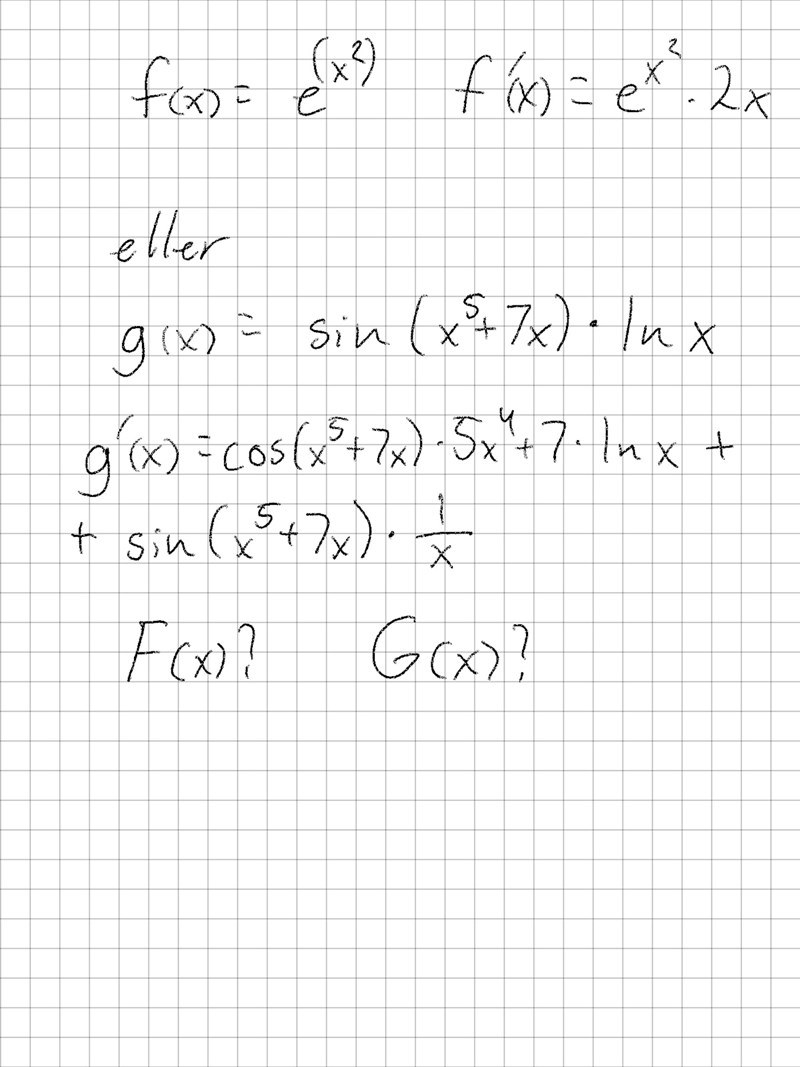
Att derivera är en regel. Att integrera är en konst.

Väldigt elegant uttryckt, @Soderstrom! Visste inte att du kunde vara så elokvent och poetisk ;)

@Themuslim7, det är alltid väldigt mycket enklare att gå framlänges än baklänges. Det gäller för ganska många saker i livet. Det är betydligt lättare att koka en god höstsoppa än att dekonstruera soppan och ta reda på vilka ingredienser som användes. Skum analogi men jag hoppas andemeningen går fram.

naytte skrev:

Väldigt elegant uttryckt, @Soderstrom! Visste inte att du kunde vara så elokvent och poetisk ;)

@Themuslim7, det är alltid väldigt mycket enklare att gå framlänges än baklänges. Det gäller för ganska många saker i livet. Det är betydligt lättare att koka en god höstsoppa än att dekonstruera soppan och ta reda på vilka ingredienser som användes. Skum analogi men jag hoppas andemeningen går fram.

Jag förstår, detta bör dock inte innebära att man inte ska försöka, vad beror det på, rent grafiskt?

Jag är osäker på hur man skulle använda ett grafiskt resonemang för att förklara varför det är svårare att integrera än att derivera. Om jag ger dig en godtycklig funktion och säger "integrera denna!" så vet du inte om jag har använt 20 deriveringsregler eller 1, inte heller vet du vilka. Då är det väl inte så konstigt att det är mycket svårare att gå åt ena hållet än andra?

Det låter rimligt. Om man först ska sätta gränser och klargöra, har ALLA funktioner endast EN derivata och vice versa (en enda primitiv funktion där bara konstanten skiljer sig)? Kan ALLA funktioner deriveras? Kan ALLA funktioner integreras? (om funktionen är kontinuerlig i alla punkter och ett x-värde inte ger två y-värden)

Alla funktioner är deriverbara och integrerbara i de intervall där de är kontinuerliga.

https://xkcd.com/2117/

naytte skrev:

Alla funktioner är deriverbara och integrerbara i de intervall där de är kontinuerliga.

Har dessa ENDAST EN derivata eller primitiv funktion (bortsett från konstanten)?

Smaragdalena skrev:

https://xkcd.com/2117/

känns inte bra i hjärtat när det är på detta vis. Kommer integralen eller derivatan av en funktion (som är kontinuerlig i alla x) bara bestå av elementära funktioner? Kan ALLA funktioner beskrivas med endast elementära funktioner?
För att sätta ännu tydligare gränser, kan man beskriva VILKEN graf SOM HELST ritat på ett kordinatsystem, som en funktion (jag syftar då på vilken ritning som helst, oavsett om den är kontinuerlig eller inte)?

Det finns integraler som inte kan anges som en elementär funktion. Ett exempel på en sådan integral är

$\displaystyle \int_{}^{}\frac{\tan x}{x}\mathrm{d}x$

En kontinuerlig funktion har endast en derivata men vissa funktioner kan ha mer än en primitiv funktion. Man får oftast med något krav i frågan så att man kan utesluta den ena.

Jag är rätt säker på att detta stämmer, men detta är frågor jag inte har funderat kring så mycket själv så någon får gärna bekräfta att det stämmer eller hojta till om det är något som inte stämmer!

naytte skrev:

Det finns integraler som inte kan anges som en elementär funktion. Ett exempel på en sådan integral är

$\displaystyle \int_{}^{}\frac{\tan x}{x}\mathrm{d}x$

En kontinuerlig funktion har endast en derivata men vissa funktioner kan ha mer än en primitiv funktion. Man får oftast med något krav i frågan så att man kan utesluta den ena.

Jag är rätt säker på att detta stämmer, men detta är frågor jag inte har funderat kring så mycket själv så någon får gärna bekräfta att det stämmer eller hojta till om det är något som inte stämmer!

Ok, så alla funktioner kan integreras så länge de är kontinuerliga (i det önskade intervallet), men det kan ha flera primitiva funktioner av samma grundfunktion? (Att det finns flera olika primitiva funktioner menar jag inte att den ena har +5 och den andra -3, alltså att de elementära funktionerna skiljer sig) varför är detta möjligt?

Vet inte hur jag ska förklara varför det är möjligt. Jag kan ge ett exempel på en situation där det finns mer än en primitiv funktion. Betrakta följande integral:

$\displaystyle \int_{}^{}\frac{1}{\sqrt{1-4x^2}}\mathrm{d}x$

Vi börjar med att ansätta följande substitution: $\displaystyle 2x=\sin\theta\implies \mathrm{d}x=\frac{1}{2}\cos\theta\mathrm{d}\theta$

Då kan vi alltså skriva om den nya integralen som:

$\displaystyle \int_{}^{}\frac{1}{2}\cdot\frac{\cos\theta}{\sqrt{\cos^2\theta}}\mathrm{d}\theta=\int_{}^{}\frac{1}{2}\cdot\frac{\cos\theta}{|\cos\theta|}\mathrm{d}\theta$

Nu har vi dock ett problem. Vi vet ingenting om $\cos\theta$. Är det negativt eller positivt? Ingen aning. Så när de "tar ut varandra" blir det antingen kvar -1 eller 1, så för att veta vilket att av dessa alternativ vi ska välja måste vi veta något om ursprungsintegralen. Där kan vi se att $\cos\theta>0$ så bråket kan uppenbarligen förkortas till 1. Men vi behövde den där ytterligare informationen, för annars fanns det två alternativ!