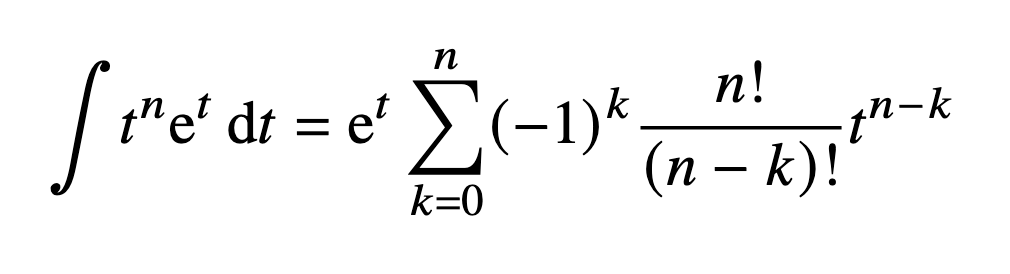Integration by parts-vart går det fel…?

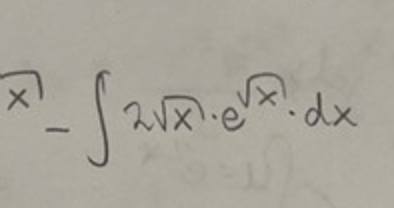
Här skall det vara 3, inte 2.

Din metod är rätt, man får "nysta sig ner" eller par gånger med P.I.

Måste rusa, kanske någon annan kan ta vid. Annars kollar jag senare i kväll på det.

Det här:

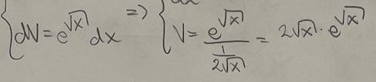
stämmer inte. Att dividera med inre derivatan funkar endast ifall inre funktionen är linjär, vilket $\sqrt{x}$ inte är.

Du får gärna kontrollera m.h.a. produkt- och kedjeregeln att $2\sqrt{x} e^{\sqrt{x}}$ inte är primitiv till $e^{\sqrt{x}}$.

Jag skulle starkt rekommendera att du gör variabelbyte i början, för att bli av med kvadratroten i exponenten. Först efter variabelbytet får du partiellintegrera.

Variabelbyte: $\sqrt{x} = t$ (där $x\ge 0$) ger $x = t^2$, så $dx = 2t\,dt$.

$\displaystyle \int x\,e^{\sqrt{x}}\,dx= [VB] = \int t^2\,e^{t}\,2t\,dt= \int 2t^3\,e^{t},dt=[PI \times 3]...$

En lämplig övning kan vara att visa