Kan man definiera funktionen som definieras av f(x)=e^x med ett supremum?

På intervallet x>=0 har vi enbart positiva termer, varför det borde gå utan vidare att definiera m h a  supremum. För negativa ser det onödigt våghalsigt ut. Ta e^-1 t ex. För komplexa går det inte för vi har ju ingen känd ordningsrelation där.

Precis som Tomten är inne på kommer detta fallera för $x<0$. Exempelvis om $x=-1$ så kommer de första delsummorna att vara

$1$

$1-1=0$

$1-1+\frac{1}{2}=\frac{1}{2}$

$1-1+\frac{1}{2}-\frac{1}{6}=\frac{1}{3}$

$1-1+\frac{1}{2}-\frac{1}{6}+\frac{1}{24}=\frac{3}{8}$

$\vdots$

WolframAlpha ger oss följande plot:

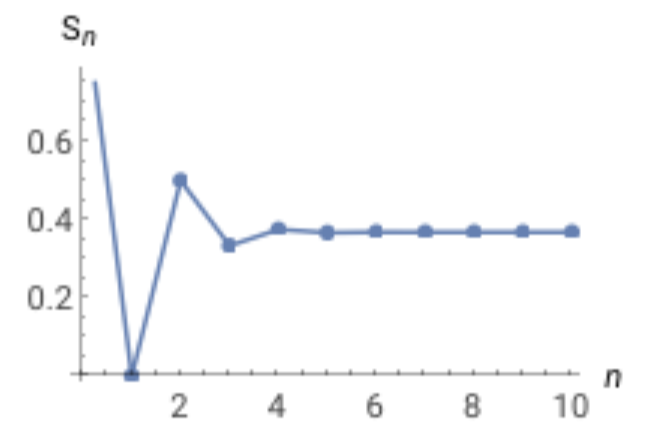
Som du ser kommer vartannan delsumma alltid att vara större än gränsvärdet $e^{-1}$. 

Om du tar supremumet av mängden av alla delsummor kommer du att få 1 (om du accepterar 0 som ett naturligt tal) eller vad nu delsumman för $n=2$ blir (om du inte accepterar 0 som ett naturligt tal).

Om du vill ha en definition med supremum som fungerar för alla $x\in\mathbb{R}$ skulle du kunna begränsa dig till de udda delsummorna, på följande vis:

   $e^x=\sup\{\sum_{k=0}^{2n+1}\frac{x^k}{k!}:n\in\mathbb{N}\}\,.$

Det kommer garantera att alla elementen i mängden är mindre än eller lika med gränsvärdet, även för $x<0$.

oggih skrev:

Om du vill ha en definition med supremum som fungerar för alla $x\in\mathbb{R}$ skulle du kunna begränsa dig till de udda delsummorna, på följande vis:

   $e^x=\sup\{\sum_{k=0}^{2n+1}\frac{x^k}{k!}:n\in\mathbb{N}\}\,.$

Det kommer garantera att alla elementen i mängden är mindre än eller lika med gränsvärdet, även för $x<0$.

Vill först bara säga att jag inte har kommit tillräckligt långt i min analysbok som handlar om funktioner som definieras som ett gränsvärde. Så detta är något jag har mycket dålig koll på.

Min första tanke med denna definition är hur den fungerar med en av exponentialfunktionens viktigaste egenskaper: den är sin egen derivata. Jag gissar att om vi har en funktion definierad enligt:

$\displaystyle f\left(x\right):= \lim_{n\to\infty}f_n\left(x\right)$ 

Så gäller det inte generellt att 

$\displaystyle f\prime\left(x\right)= \lim_{n\to\infty}f_n\prime\left(x\right)$

Min gissning är att detta gäller för vissa sekvenser som konvergerar på något trevligt sätt eftersom det vi gör när vi tar respektive derivata är att byta ordning på två grönsvärden. Men hur som helst, vi har i alla fall inte gränsvärdet av en sekvens i detta fall.

Om vi låter

$\displaystyle g_n\left(x\right):= \sum_{k=0}^{n}\frac{x^k}{k!}$

så har vi att 

$\displaystyle e^x =\lim_{n\to\infty}g_n\left(x\right)$

och om man tar derivatan av respektive $g_n$ gäller gränsvärdet ovan fortfarande. Trevligt! Gällde supremum-definitionen har har vi enligt @oggih:

$\displaystyle e^x=\sup\{g_{2n+1}\left(x\right):n\in\mathbb{N}\}$

Om man då skulle, naivt, testa att ta derivatan av varje funktion i mängden skulle likheten inte längre hålla. Finns det något enkelt sätt att ta derivatan av funktionen enligt denna supremum-definition?

Drar mig till minnes att om konvergensen är likformig över ngn mängd, så får elementen i en följd både deriveras och integreras med gränsens derivata/integral som resultat. (Möjligen krävs även att mängden är kompakt, har inte min gamla mattebibel i närheten för exakt koll).

Intressant förslag, @oggih!

Har någon något snyggt resonemang för att visa att supremet till mängden av alla udda delmängder för något $x\in \mathbb{R}$ faktiskt kommer vara $e^x$? Det är klart att det är en majorant (en udda delsumma är ju alltid en underapproximation) men har någon något fiffigt sätt att visa att detta definierar samma funktion som det klassiska gränsvärdet?

Det skulle kanske kunna vara en nyttig övning för dig själv att visa följande allmänna resultat! ^_^

Proposition. Låt $(a_n)_{n=1}^\infty$ vara en växande följd av reella tal, och låt $b$ vara ett reelt tal. Då gäller att $b=\lim_{n\to\infty} a_n$ om och bara om $b=\sup\{a_n\mid n\in\mathbb{Z}_{\geq 0}\}$.

Gäller det generellt för växande följder? Har skissat lite på ett bevis och det känns som att det endast borde gälla generellt om följden är strikt växande.

Jag tror inte att följden behöver vara strikt växande, men du kan för all del börja med det antagandet (det är allt vi behöver för vårt problem med e^x), och så kan vi diskutera om beviset kan anpassas till icke-strikt växande följder senare.

Jag tror att jag fick ihop något även utan antagandet att följden är strikt växande. Vi får se om det är på rätt spår. Tyvärr är jag på landet utan dator så att formatera allting snyggt i LaTeX hade tagit en evighet, varför jag skickar mitt försök som bild:

Tillägg: 25 jul 2025 10:03

Jag ser nu att jag har missbrukat ordet „ekvivalent“. Jag menade implikation.

Bump. Är det rätt idé i försöket eller är jag helt ute och cyklar (bortsett från att jag har skrivit „ekvivalent” och „omformulera“ lite slarvigt)?

Nu när jag är hemma igen kan jag formatera ett ordentligt svar. I det här inlägget försöker jag korrigera de fel och oprecisheter som förekom i mitt tidigare försök. Jag vill också inleda med en liten kort kommentar av en karaktärisering av supremumfunktionen $\sup$ som jag har använt i min text ovan men inte motiverat. Låt $\sim$ innebära att två samband (ekvationer och olikheter) är ekvivalenta (vi inför denna symbol för att slippa förvirring med andra logiska symboler som $\Longleftrightarrow$).

Supremet defineras klassiskt som den minsta övre begränsningen för en uppåt begränsad mängd. Låt $S\subseteq \mathbb{R}$ vara någon uppåt begränsad mängd. Då säges $a\in\mathbb{R}$ vara supremet till $S$ (skrives $\sup S = a$) om och endast om $a \ge b$ för alla $b\in S$ samt $a < c$ för alla andra övre begränsningar $c\in\mathbb{R}$.

En ekvivalent karaktärisering av denna definition är följande:

$\displaystyle \sup S=a \Longleftrightarrow \left(\forall s\in S\right): s\le a \; \wedge \; \left(\forall\varepsilon >0\right)\left(\exists s\in S\right):a-\varepsilon< s$

Vi kan bevisar detta genom att visa att negationen till detta påstående är falsk:

Antag att $a = \sup S$ enligt den klassiska karaktäriseringen. Antag att det finns ett $\varepsilon > 0$ sådant att $a-\varepsilon \ge s$ för alla $s\in S$. Då är $a' = a-\varepsilon$ också en övre begränsning till $S$, och eftersom vi vet att $a$ är supremet till $S$ måste vi ha $a<a'=a-\varepsilon$, vilket är omöjligt. Således måste vi ha:

$\displaystyle \sup S=a \Longleftrightarrow\left(\forall\varepsilon >0\right)\left(\exists s\in S\right):a-\varepsilon< s$

Sats

Låt $\displaystyle (a_n)_{n=1}^{\infty}$ vara en växande följd. Då gäller att $b=\lim_{n\to\infty}a_n$ om och endast om $\displaystyle b=\sup\{a_n:n\in\mathbb{N}\}$

($\displaystyle \Longrightarrow$):

Antag att $b=\lim_{n\to\infty} a_n$. Då har vi per definition:

$\displaystyle (i)\;\;\; \left(\forall\varepsilon>0\right)\left(\exists N\in\mathbb{N}\right):n\ge N\Longrightarrow \left|b-a_n\right|<\varepsilon$

Eftersom följden är växande vet vi att $b\ge a_n$ för alla $n$. Vi har således $n \ge N  \Longrightarrow b-a_n < \varepsilon$. Eftersom vi vet att det för varje $\varepsilon >0$ finns ett $N\in\mathbb{N}$ vet vi också att det för varje $\varepsilon > 0$ finns ett $a_n$ sådant att $b-a_n < \varepsilon$. Det följer alltså från $(i)$ att:

$\displaystyle (ii)\;\;\; \left(\forall\varepsilon>0\right)\left(\exists a_n\in\{ a_n:n\in\mathbb{N} \}\right):b-a_n<\varepsilon \sim b-\varepsilon < a_n$

vilket enligt utläggningen ovan precis är definitionen för att $b = \sup\{ a_n:n\in\mathbb{N} \}$

($\displaystyle \Longleftarrow$):

Antag att $b = \sup\{ a_n:n\in\mathbb{N} \}$. Enligt karaktäriseringen ovan vet vi då alltså att:

$\displaystyle (iii)\;\;\; \left(\forall\varepsilon>0\right)\left(\exists a_n\in\{ a_n:n\in\mathbb{N} \}\right): b-\varepsilon < a_n$

Eftersom följden är växande ($a_n \ge a_N$ för  $n\ge N$) vet vi att för alla $n\ge N$, givet $\varepsilon >0$, att $b-\varepsilon < a_n$. $(iii)$ implicerar således:

$\displaystyle \displaystyle (iiii)\;\;\; \left(\forall\varepsilon>0\right)\left(\exists N\in\mathbb{N}\right):n\ge N\Longrightarrow b-\varepsilon < a_n \sim \left|b-a_n\right| <\varepsilon$

vilket är precis definitionen för att $b=\lim_{n\to\infty}a_n$.

Eftersom vi har $\displaystyle b=\sup\left\{ a_n:n\in\mathbb{N} \right\}\Longrightarrow b=\lim_{n\to\infty}a_n$ samt $\displaystyle b=\lim_{n\to\infty}a_n \Longrightarrow b=\sup\left\{ a_n:n\in\mathbb{N} \right\}$, har vi $\displaystyle b=\lim_{n\to\infty}a_n \Longleftrightarrow b=\sup\left\{ a_n:n\in\mathbb{N} \right\}$, vilket slutför beviset.

$\blacksquare$

EDIT: fixade ett fel om karaktäriseringen av supremumfunktionen.

Jag har inte haft tid att läsa ditt svar ordentligt, men jag kom att tänka på ett alternativt sätt att definiera exponentialfunktionen, som indirekt bygger på sup och inf, och som (så vitt jag kan se) inte involverar gränsvärden:

• Börja med att definiera den naturliga logaritmfunktionen $\ln\colon\mathbb{R}_{>0}\to\mathbb{R}$ genom Riemannintegralen ${\ln(x)}=\int_0^x \frac{1}{t}\,\mathrm{d}t$, där vi kan tänka oss att vi har definierat Riemannintegralen på det vanliga sättet med sup och inf av över- och undersummor.
• Övertyga dig om att logartimen är en bijektion.
• Definiera exponentialfunktion $\exp\colon\mathbb{R}\to\mathbb{R}_{>0}$ som inversen till $\ln\colon\mathbb{R}_{>0}\to\mathbb{R}$.

Det är en väldigt trevlig och geometrisk definition, men utmaningen är så klart nu att visa att här "versionen" av exponentialfunktionen har alla önkvärda egenskaper (inklusivse identiteten ${\exp(x)}=\sum_{k=0}^\infty x^k/k!$). Det är kanske inte direkt något man gör i en handvändning, men är rätt säker på att jag har sett analysläroböcker som utgår från den här definitionen utan större pedagogiska problem.

Tillägg: 28 jul 2025 23:50

När jag skrev "det vanliga sättet" så menar jag det som ibland kallas för darbouxintegraler (lärde mig precis det ordet av nayttes andra tråd!).

Ah, trevlig idé! Jag tror faktiskt det var så vi gjorde i vår kurs i envariabelanalys på universitet, men då bekymrade vi oss inte över huruvida vår variant av funktionen faktiskt hade alla önskvärda egenskaper, utan vi tog det för givet. Hur som helst ett mycket trevligt förslag! :D

bump