Kan man inte tillämpa detta bevis av Carnots sats på vilken pump som helst?

Halloj!

Jag håller på att försöka försåt Carnots sats som säger att det inte finns någon värmemotor som har högre verkningsgrad än Carnotmotorn, samt att det inte finns någon värmepump som har högre verkningsgrad än Carnotpumpen. I beviset jag hittade här argumenterar de så här:

Antag att vi kopplar ihop en Carnotpump med en (eventuellt irreversibel) väremotor enligt figur:

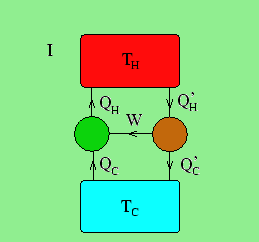
För att vi inte ska bryta mot termodynamikens andra huvudsats kräver vi att $Q_H^\prime \ge Q_H$. Verkningsgraden för värmemotorn kan skrivas:

$\displaystyle \eta_{\text{irr.}}=\frac{W}{Q_H^\prime}=\frac{Q_H}{Q_H}\cdot\frac{W}{Q_H^\prime}=\frac{Q_H}{Q_H^\prime}\cdot\frac{W}{Q_H}\le\eta_{\text{Carnot}}$

Men var någonstans i det här argumentet har vi använt att pumpen är en reverserad Carnotmotor? Hade inte samma argument fungerat på en godtycklig värmepump?