3
svar
144
visningar
Zeshen är nöjd med hjälpen
Kärna eller kernel av en operator L
Har jag tänkt rätt på operationen? Eller ska det vara som i rött.
Hur uttrycker jag basen? Ska man definiera en egen bas?
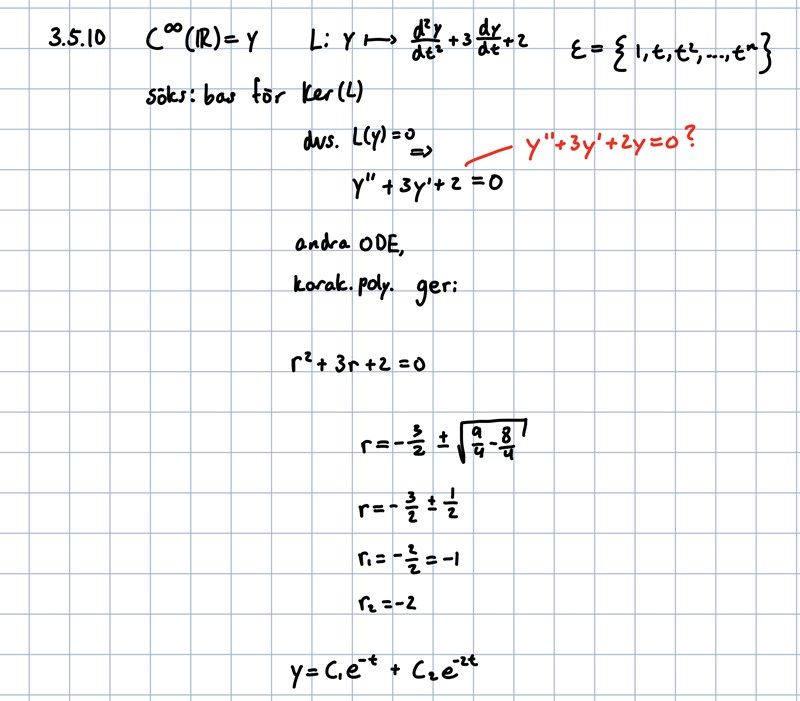
Hej,
Ja, du har funnit att operatorns nollrum har basen .
Angående tolkningen av operatorn fungerar den såhär: Funktionen kopplas ihop med funktionen där
.
Albiki skrev:Angående tolkningen av operatorn fungerar den såhär: Funktionen kopplas ihop med funktionen där
.
Ah, tack! Så man tänker att man multiplicerar L med y(t)

