Kedjeregeln

1/g(x) är också en funktion, som du kan kalla för något. k(x) kanske. Så h(x) = f(k(x)), och då säger definitionen att

$h^\prime \left(x\right) = f^\prime \left(k\left(x\right)\right) \cdot k^\prime \left(x\right) = f^\prime \left(\frac{1}{g(x)}\right) \cdot k^\prime \left(x\right)$.

Återstår att bestämma derivatan k'(x)! Så vad är derivatan av 1/g(x)?

Sätt $a\left(x\right)=\frac{1}{g\left(x\right)}$. Då är $h\text{'}\left(x\right)=f\text{'}\left(a\right(x\left)\right)·a\text{'}\left(x\right)$. Då behöver vi bara hitta $a\text{'}\left(x\right)$. Vi kan skriva om $a\left(x\right)=\frac{1}{g\left(x\right)}={\left(g\left(x\right)\right)}^{-1}$. Nu kan vi använda kedjeregeln igen på detta uttryck för att hitta $a\text{'}\left(x\right)$. :)

Smutstvätt skrev:

Sätt $a\left(x\right)=\frac{1}{g\left(x\right)}$. Då är $h\text{'}\left(x\right)=f\text{'}\left(a\right(x\left)\right)·a\text{'}\left(x\right)$. Då behöver vi bara hitta $a\text{'}\left(x\right)$. Vi kan skriva om $a\left(x\right)=\frac{1}{g\left(x\right)}={\left(g\left(x\right)\right)}^{-1}$. Nu kan vi använda kedjeregeln igen på detta uttryck för att hitta $a\text{'}\left(x\right)$. :)

Hej, här är uppgiften, 3146 b). Förstår fortfarande inte riktigt vad ni menar!!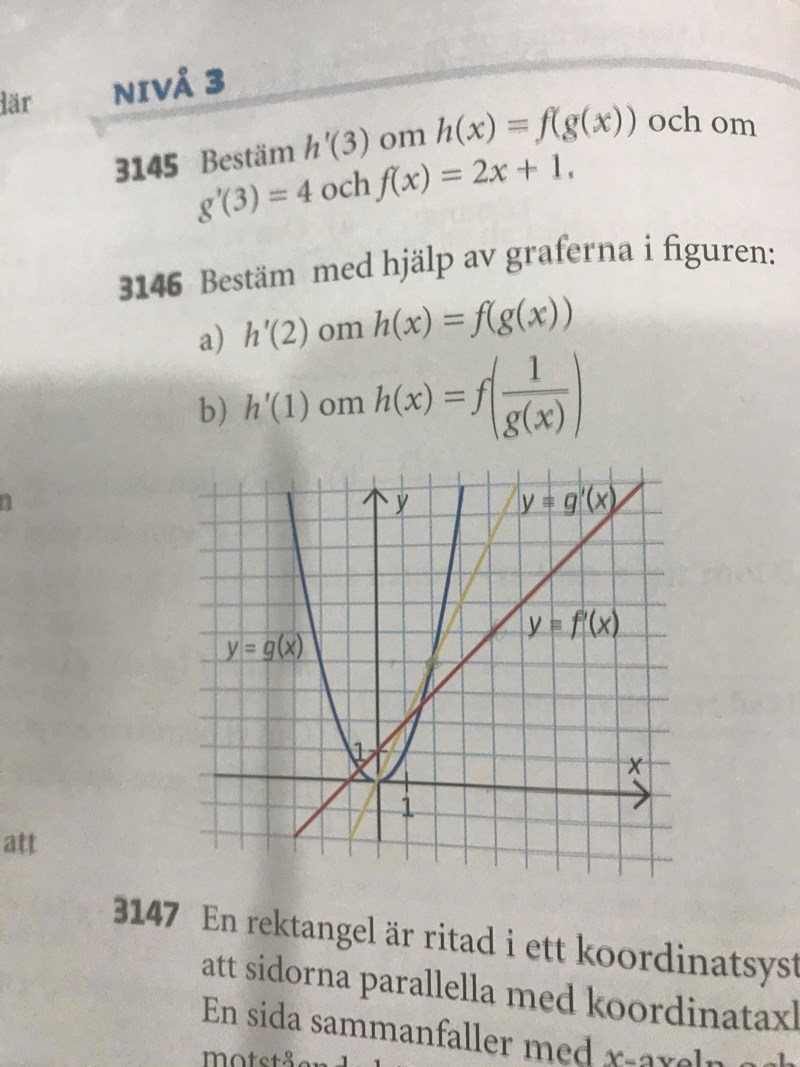

Vilka analytiska uttryck har g(x) och f'(x) ? Det kan du få fram från figuren.

oneplusone2 skrev:

Vilka analytiska uttryck har g(x) och f'(x) ? Det kan du få fram från figuren.

g(x)=x^2 och f'(x)=x+1

De har infört en rättning på den här uppgiften. "Linjerna f'(x) och g'(x) ska byta namn."

Lite förvirrande annars.

Om du inte har rättelserna så sök på lärobokens hemsida så får du dem. Det är mycket värdefullt att ha dem.

ConnyN skrev:

De har infört en rättning på den här uppgiften. "Linjerna f'(x) och g'(x) ska byta namn."

Lite förvirrande annars.

Om du inte har rättelserna så sök på lärobokens hemsida så får du dem. Det är mycket värdefullt att ha dem.

Ok, men jag får ju faktiskt rätt svar om jag går efter det som står i boken? 

villsovaa skrev:

ConnyN skrev:

De har infört en rättning på den här uppgiften. "Linjerna f'(x) och g'(x) ska byta namn."

Lite förvirrande annars.

Om du inte har rättelserna så sök på lärobokens hemsida så får du dem. Det är mycket värdefullt att ha dem.

Ok, men jag får ju faktiskt rätt svar om jag går efter det som står i boken? 

Ajdå. Jag kollade min lösning, men den ser ut att ge fel svar? Av någon anledning så lämnade jag uppgiften så. Det brukar jag inte göra.
Kanske du kan ge mig tips på var felen ligger?
Både a och b är fel.

Skulle vara roligt om du delade med dig av din lösning.

ConnyN skrev:

villsovaa skrev:

Visa föregående citat

ConnyN skrev:

De har infört en rättning på den här uppgiften. "Linjerna f'(x) och g'(x) ska byta namn."

Lite förvirrande annars.

Om du inte har rättelserna så sök på lärobokens hemsida så får du dem. Det är mycket värdefullt att ha dem.

Ok, men jag får ju faktiskt rätt svar om jag går efter det som står i boken? 

Ajdå. Jag kollade min lösning, men den ser ut att ge fel svar? Av någon anledning så lämnade jag uppgiften så. Det brukar jag inte göra.
Kanske du kan ge mig tips på var felen ligger?
Både a och b är fel.

Skulle vara roligt om du delade med dig av din lösning.

Grejen är att jag inte tror att man kan tillämpa kedjeregeln enligt definition på samma sätt i b), eftersom g(x) inte är den inre funktionen längre utan tex k(x)=1/g(x) är det istället, vilket jag fick hjälp med av pluggakuten i den här tråden igår. Därför blir din lösning nog fel. Mina lösningar på både a och b kommer här: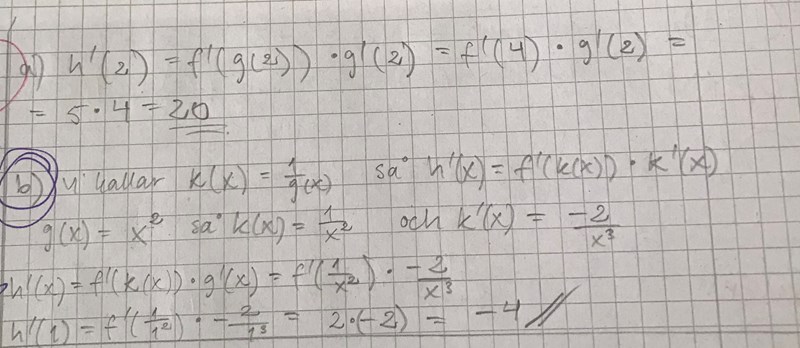

Den här var värre än jag trodde, men Smutstvätt och du verkar att hitta en genväg som jag inte är helt med på.

Så här ser mitt tänk ut nu:

1) Inre funktion är g(x) = x² = z ; inre deriverad funktion är g'(x) = 2x; yttre deriverad funktion är f'(z) = z + 1

2) uppgift a) $h\text{'}\left(x\right)=(x^2+1)·2x=2x^3+2x$och h'(2) = 20 vilket vi båda har fått fram, men facit har 24.

3) uppgift b) inre funktion är $g\left(x\right)=\frac{1}{x^2}=z;$yttre deriverad funktion är fortfarande $f\left(z\right)=z+1$
     deriverad inre funktion är $g\text{'}\left(x\right)=-\frac{2}{x^3}$deriverad yttre funktion är $f\text{'}\left(x\right)=\frac{1}{x^2}+1$

4) $h\text{'}\left(x\right)=(\frac{1}{x^2}+1)·(-\frac{2}{x^3})$och $h\text{'}\left(1\right)=(1+1)·(-2)=-4$
Kanske jag är ute och cyklar nu? Skulle vara mycket tacksam för assistans, som sagt jag är inte med på Smutstvätt och din beräkning av b)

ConnyN skrev:

Den här var värre än jag trodde, men Smutstvätt och du verkar att hitta en genväg som jag inte är helt med på.

Så här ser mitt tänk ut nu:

1) Inre funktion är g(x) = x² = z ; inre deriverad funktion är g'(x) = 2x; yttre deriverad funktion är f'(z) = z + 1

2) uppgift a) $h\text{'}\left(x\right)=(x^2+1)·2x=2x^3+2x$och h'(2) = 20 vilket vi båda har fått fram, men facit har 24.

3) uppgift b) inre funktion är $g\left(x\right)=\frac{1}{x^2}=z;$yttre deriverad funktion är fortfarande $f\left(z\right)=z+1$
     deriverad inre funktion är $g\text{'}\left(x\right)=-\frac{2}{x^3}$deriverad yttre funktion är $f\text{'}\left(x\right)=\frac{1}{x^2}+1$

4) $h\text{'}\left(x\right)=(\frac{1}{x^2}+1)·(-\frac{2}{x^3})$och $h\text{'}\left(1\right)=(1+1)·(-2)=-4$
Kanske jag är ute och cyklar nu? Skulle vara mycket tacksam för assistans, som sagt jag är inte med på Smutstvätt och din beräkning av b)

Hej, först och främst så säger mitt facit att svaret är 20 på a). Ditt facit kanske möjligen råkar vara fel?

Sen så kanske vi borde invänta svar från smutstvätt för en bra förklaring, men jag kan försöka förklara lite hur jag tänkt utifrån tipset som smutstvätt gav mig.

Du säger att den inre funktionen är g(x). Den kan inte vara g(x), då det inte gäller för definitionen av kedjeregeln. Definitionen av kedjeregeln lyder som följer:

h'(x) = f'(g(x)) * g'(x) där h(x) = f(g(x))

Men eftersom frågan säger att h(x) = f(1/g(x)) så kan vi inte använda samma beteckningar som användes för definitionen. För att Definitionen ska gälla, inför vi en ny variabel k. Vi låter vår omskrivna definition se ut som följande:

h'(x) = f'(k(x)) * k'(x) där h(x) = f(k(x)) och där vi nu sätter k = 1/g(x). Nu stämmer det med variabler och definition. k(x) är vår inre funktion.

Sen är det bara att räkna.

yttre funktion/derivata:

k(x) = 1/g(x) = 1/$x^2$

som ger

k(1) = 1/g(1) = 1/$1^2$  = 1

Som ger den första faktorn i vår definition:

f'(k(x)) = f'(1/g(x)) 

f'(k(1)) = f'(1) = 2 så nu är den första faktorn i kedjeregelns definition klar. Vi kommer att använda den sen. 

Nästa faktor, k'(x), ges av följande:

yttre funktion/derivata:

k(x) = 1/g(x) = 1/$x^2$

Då blir k'(x) = -2($x^{-3}$ ) = -2/$x^3$

Den andra faktorn i definitionen blir då:

k'(x) = -2/$x^3$      

som ger

k'(1) = -2/$1^3$ = -2

Vi sätter in dessa i definitionen h'(x) = f'(k(x)) * k'(x) Och då blir:

h'(1) = f'(k(1)) * k'(1) = 2 * -2 = -4

Så här har jag tänkt, baserat på det jag kunde tolka av hjälpen jag fick i den här tråden!

Tack så hemskt mycket för svaret.
Nu förstår jag också både Skafts Smutstvätts svar bättre, men övergången till att få den yttre derivatan till 2 förstår jag inte.
Vi har $f\text{'}\left(\frac{1}{g\left(x\right)}\right)=f\text{'}(g{\left(x\right))}^{-1}=-(g{\left(x\right))}^{-2}=-\frac{1}{(g{\left(x\right))}^2}$ om jag nu förstått rätt? men sedan?

(Konstigt med svaret på a) vilken upplaga har du? Jag har upplaga 2 tryckning 2 från 2013. Jag tvivlar inte på att 20 är rätt, men undrar ändå eftersom jag inte hittar någon rättning av det)

Är det så här?

Först har vi $h\left(x\right)=f\left(g\right(x\left)\right)$med $g\left(x\right)=x^2=z$
derivatan av den inre funktionen $g\text{'}\left(x\right)=2x$
och derivatan av den yttre funktionen $f\text{'}\left(z\right)=z+1$
vilket då ger $h\text{'}\left(x\right)=(x^2+1)·2x$

I fråga b) har vi $h\left(x\right)=f\left(\frac{1}{g\left(x\right)}\right)=f\left(\right(g{\left(x\right))}^{-1})$
det ger derivatan av den inre funktionen till $f\text{'}\left(x\right)=-\frac{2}{x^3}$
och den yttre är oförändrat $f\text{'}\left(z\right)=z+1$
då får vi $h\text{'}\left(x\right)=(\frac{1}{x^2}+1)·(-\frac{2}{x^3})$
och då får vi $h\text{'}\left(1\right)=-4$

ConnyN skrev:

Är det så här?

Det ser bra ut!

Notera dock att man inte behöver bestämma funktionsuttrycken. Det är ett bra sätt att föra över problemet på "bekant mark", men det räcker egentligen att vi har f', g och g' skissade så vi kan läsa av dess värden.

På a) använder vi kedjeregeln direkt och skriver $h^\prime(x) = f^\prime(g(x))\cdot g^\prime(x)$. Sätter vi in x=2 får vi att

$h^\prime(2) = f^\prime(g(2))\cdot g^\prime(2)$

I bilden ser vi att g(2) = 4 och g'(2) = 4. Så:

$h^\prime(2) = f^\prime(4)\cdot 4$

Och i bilden läser vi av f'(4) = 5. Så:

$h^\prime(2) = 5\cdot 4 = 20$

På samma sätt kan man lösa b) genom att derivera h "generellt" med hjälp av kedjeregeln, och sen bestämma h'(1) genom att läsa av relevanta värden ur bilden och sätta in i uttrycket man hittat.

Skaft skrev:

ConnyN skrev:

Är det så här?

Det ser bra ut!

Notera dock att man inte behöver bestämma funktionsuttrycken. Det är ett bra sätt att föra över problemet på "bekant mark", men det räcker egentligen att vi har f', g och g' skissade så vi kan läsa av dess värden.

På a) använder vi kedjeregeln direkt och skriver $h^\prime(x) = f^\prime(g(x))\cdot g^\prime(x)$. Sätter vi in x=2 får vi att

$h^\prime(2) = f^\prime(g(2))\cdot g^\prime(2)$

I bilden ser vi att g(2) = 4 och g'(2) = 4. Så:

$h^\prime(2) = f^\prime(4)\cdot 4$

Och i bilden läser vi av f'(4) = 5. Så:

$h^\prime(2) = 5\cdot 4 = 20$

På samma sätt kan man lösa b) genom att derivera h "generellt" med hjälp av kedjeregeln, och sen bestämma h'(1) genom att läsa av relevanta värden ur bilden och sätta in i uttrycket man hittat.

Skaft, så man kan fortfarande tillämpa kedjeregeln direkt på b) utan att "substituera" med tex k(x)? Praktiskt! Skulle du kunna visa hur man gör? 

och ConnyN, jag har andra upplagan, fjärde tryckningen av boken, också från 2013. Så det kanske är ändrat i efterhand!

k(x) är ju så att säga bara ett namnbyte. Jag (och andra) lägger in såna ibland för att förtydliga "det här är ett eget funktionslager". Men man behöver inte göra så. Ett annat notationssätt är D(nån funktion) för att beteckna "derivatan av nån funktion". Använder vi det kan vi uttrycka kedjeregeln på b) så här:

$h^\prime\left(x\right) = f^\prime\left(\dfrac{1}{g(x)}\right)\cdot D\left(\dfrac{1}{g(x)}\right)$

Ett alternativt skrivsätt, men logiken är helt densamma: multiplicera f' med derivatan av vad som står inuti f()-parenteserna. Derivatan av 1/g(x) kan man t.ex. med kvotregeln få till -g'(x) / g(x)^2, (eller också genom att skriva om till g(x)^-1 och ta kedjeregeln igen). Sätt in resultatet:

$h^\prime\left(x\right) = f^\prime\left(\dfrac{1}{g(x)}\right)\cdot \left(-\dfrac{g^\prime\left(x\right)}{g\left(x\right)^2}\right)$

Så för x=1:

$h^\prime\left(1\right) = f^\prime\left(\dfrac{1}{g(1)}\right)\cdot \left(-\dfrac{g^\prime\left(1\right)}{g\left(1\right)^2}\right)$

Läs av värden, sätt in, etc =)

Skaft skrev:

k(x) är ju så att säga bara ett namnbyte. Jag (och andra) lägger in såna ibland för att förtydliga "det här är ett eget funktionslager". Men man behöver inte göra så. Ett annat notationssätt är D(nån funktion) för att beteckna "derivatan av nån funktion". Använder vi det kan vi uttrycka kedjeregeln på b) så här:

$h^\prime\left(x\right) = f^\prime\left(\dfrac{1}{g(x)}\right)\cdot D\left(\dfrac{1}{g(x)}\right)$

Ett alternativt skrivsätt, men logiken är helt densamma: multiplicera f' med derivatan av vad som står inuti f()-parenteserna. Derivatan av 1/g(x) kan man t.ex. med kvotregeln få till -g'(x) / g(x)^2, (eller också genom att skriva om till g(x)^-1 och ta kedjeregeln igen). Sätt in resultatet:

$h^\prime\left(x\right) = f^\prime\left(\dfrac{1}{g(x)}\right)\cdot \left(-\dfrac{g^\prime\left(x\right)}{g\left(x\right)^2}\right)$

Så för x=1:

$h^\prime\left(1\right) = f^\prime\left(\dfrac{1}{g(1)}\right)\cdot \left(-\dfrac{g^\prime\left(1\right)}{g\left(1\right)^2}\right)$

Läs av värden, sätt in, etc =)

Stort tack, Skaft! Nu förstår jag mycket bättre!

Tack till Skaft för klargörande och tack till villsovaa som fick mig att "grotta" ner mig.

Som du konstaterat villsovaa så har de rättat både bild och svar i din utgåva.
Orsaken att jag lade ner uppgiften var nog att det blev så totalt förvirrande med de felen plus att
jag tycker att detta var en av de mer förvirrande sakerna i hela kapitlet, men nu har det ljusnat en hel del
tack vare detta. 😊