Kedjeregeln och inre samt yttre funktion

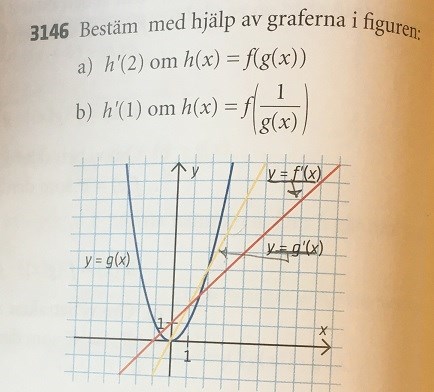
Jag använder mig på början av Geogebra för att rekonstruera bilden från boken och på det sättet bestämma funktionerna till g(x), f(x), g´(x) och f´(x)

Från boken ser vi att g(x) = x^2. Dess derivata g`(x) måste då vara 2x. Vi ser att f´(x) är en rät linje. Därför sätter jag in värdet x i geogebra och jämför de båda funktionerna. För att gå vidare härifrån måste du använda dig av det du lärt dig i det tidigare kapitlet Trigonometri-förflyttning av grafer. Där lärde vi oss att för att förflytta en graf åt vänster adderar vi en konstant. I det här fallet ser vi att funktionen skär i -1 därför är f´(x) = x+1.

Nu kan du använda dig av antiderivat för att bestämma f(x) =( x^2)/2 +x. f(g(x)) = ((x^2)^2)/2 +x^2 = (x^4)/2 + x^2.

I den här uppgiften finns ingen inre och yttre funktion. Du deriverar delarna separat.

h´(x) = (4x^3)/2+2x = 2x^3+2x då blir h´(2)=20

Hej Conny,

Din beräkning säger felaktigt att derivatan $h^\prime(x)$ är $f^\prime(g(x))$. Den korrekta beräkningen enligt Kedjeregeln är

    $h^\prime(x)=f^\prime(g(x)) \cdot g^\prime(x).$

Med $f^\prime(x) = x+1$ blir $f^\prime(g(x)) = g(x)+1$ och $g^\prime(x) = 2x$ fås resultatet $h^\prime(2) = (1+2^2) \cdot 4=20.$ 

Om man istället felaktigt använder $f^\prime(x) = 2x$ fås resultatet $h^\prime(2)=(2\cdot 2^2)\cdot 4=32.$

Det verkar som att facit är fel.

Wiki skrev:

Jag använder mig på början av Geogebra för att rekonstruera bilden från boken och på det sättet bestämma funktionerna till g(x), f(x), g´(x) och f´(x)

Från boken ser vi att g(x) = x^2. Dess derivata g`(x) måste då vara 2x. Vi ser att f´(x) är en rät linje. Därför sätter jag in värdet x i geogebra och jämför de båda funktionerna. För att gå vidare härifrån måste du använda dig av det du lärt dig i det tidigare kapitlet Trigonometri-förflyttning av grafer. Där lärde vi oss att för att förflytta en graf åt vänster adderar vi en konstant. I det här fallet ser vi att funktionen skär i -1 därför är f´(x) = x+1.

Nu kan du använda dig av antiderivat för att bestämma f(x) =( x^2)/2 +x. f(g(x)) = ((x^2)^2)/2 +x^2 = (x^4)/2 + x^2.

I den här uppgiften finns ingen inre och yttre funktion. Du deriverar delarna separat.

h´(x) = (4x^3)/2+2x = 2x^3+2x då blir h´(2)=20

Intressant att se ett helt annat sätt att lösa det på och glädjande att vi kommer till samma svar.
Själv har jag med två olika sätt att använda kedjeregeln, Börje Sundvalls och min läroboks sätt löst och kommit till samma resultat att h'(2) = 20  Det som skiljer de två metoderna åt är mer behandlingen av funktionsbeteckningar. Den jag använt ovan är lärobokens som jag tycker är bra.

Tack för svaret och ett nytt tips!

Albiki skrev:

Hej Conny,

Din beräkning säger felaktigt att derivatan $h^\prime(x)$ är $f^\prime(g(x))$. Den korrekta beräkningen enligt Kedjeregeln är

    $h^\prime(x)=f^\prime(g(x)) \cdot g^\prime(x).$

Med $f^\prime(x) = x+1$ blir $f^\prime(g(x)) = g(x)+1$ och $g^\prime(x) = 2x$ fås resultatet $h^\prime(2) = (1+2^2) \cdot 4=20.$ 

Om man istället felaktigt använder $f^\prime(x) = 2x$ fås resultatet $h^\prime(2)=(2\cdot 2^2)\cdot 4=32.$

Det verkar som att facit är fel.

Ja där rörde jag till det, men beräkningen är riktig. Det är som jag skriver i svaret ovan att det är min lärobok som använder beteckningen f(z) för den yttre funktionen, vilket underlättar för mig. Det blir många x annars. Som jag skrev så kan man också följa ett mönster som Börje Sundvall använder i sina föreläsningar på YouTube.
Jag upplever att du har en annan variant även om den är närmare Börjes alternativ, men som du ser får du och jag exakt samma resultat för h'(2)

Tack så mycket för svaret! Nu börjar jag bli övertygad om att jag gjort rätt. Även om jag känner mig som nybörjare med dessa beteckningar på funktionerna. Det är ganska lätt att komma fel där tycker jag, men det är som vanligt mer träning som gäller eller som Neil Young uttryckte det "jag tränar aldrig, jag bara spelar" Vad är skillnaden kan man fråga 😊