Kinetisk energi för "dubbelpendel"
.jpg?width=800&upscale=false)
Hej!
Jag har problem med att ställa upp den kinetiska energin i denna uppgift. Jag tänker att ringen har en rotationsenergi , men insektens energi är lite lurigare. Den har ju dels en hastighet , men hur skall jag relatera ringens hastighet till insekten? Först tänkte jag att insekten ju står på ringen, och därför har total hastighet , men det blir fel och liknar vid närmare eftertanke inte alls dubbelpendeln. I dubbelpendeln kan man ju se det som att den övre delen ger en hastighet år den nedre, och sedan att den nedre har en egen hastighet (se bild nedan). Om man sedan adderar dessa hastighetsvektorer får man en total hastighetsvektor för den nedre massan, som fås med cosinussatsen. Men hur skall man tänka i de banorna i den här uppgiften? Jag vet inte riktigt hur jag skall tänka eftersom mittpunkten är fix här, medan både den övre och nedre punkten rör sig.
Man kanske kan tänka sig att den övre punkten rör sig med hastighet och den nedre med relativt den övre delen, och sedan addera vektorerna m.h.a. cosinussatsen. Men även när jag gör det får jag fel svar (trots att det denna gång blir "identiskt med den för dubbelpendeln").
Nedan följer en bild på dubbelpendeln samt uttrycket för dess kinetiska energi:
.jpg?width=800&upscale=false)
.jpg?width=800&upscale=false)
I vårt fall är alltså och , och .
Spännande uppgift. Vad säger kompendiet om att byta ut till en generaliserad koordinat? Det verkar vara en ledning som löser uppgiften åt dig.
Energin för disken är i detta fall:
, där är masströghetsmomentet för en disk som roterar kring en axel i sitt periferi.
Jag är lite fundersam på detta som du skriver:
pixisdot skrev:
...eftersom mittpunkten är fix här, medan både den övre och nedre punkten rör sig.
Jag tolkar det som att disken sitter fast i övre periferin och roterar kring den, inte att den roterar kring sin mittpunkt. Om du kollar på uppgiften står det:
Disken roterar fritt runt en axel genom kanten
Insekten har mycket riktigt en hastighet relativt disken som är , där är en tangentialvektor ortogonal till , men sedan har den även en rörelse relativt den fixerade axeln eftersom punkten som vektorn utgår från rör sig. Kan du beskriva hur varierar med tiden? Du vet att mittpunkten hos disken rör sig med hastigheten , där är en tangentialvektor ortogonal till . Den absoluta hastigheten hos insekten bör således bli:
Det knepiga här är att beskriva tangentialvektorerna i termer av vinklarna men det kan du nog lista ut.
Aah, hur kunde jag missa att rotationsaxeln inte var i centrum... Jag ska försöka lösa uppgiften imorgon igen, det borde gå bra med din hjälp! Tack :)
En sak jag är fundersam på är det här med generaliserad koordinat. Vad menar de med "...ingen symmetri kring upphängningsaxeln...", tror du? Jag skulle inte påstå att det blir enklare att byta ut koordinaten på något vis, snarare tvärtom då det blir mer omständligt.
Vinkeln mot insekten kan utgå från var som helst på ringen så den skulle kunna vara eller vad som helst. Det är bara ett uttryck för dess position relativt en diameter i ringen. Jag skulle vara väldigt intresserad av att se din lösning på uppgiften.
Jag försökte svara igår men posten publicerades aldrig, får se om det går bättre idag.
Jag vet faktiskt inte vad de menar med "symmetri kring upphängningsaxeln", man borde kunna använda de koordinater som de använder i kompendiet (där det stod om dubbelpendeln) och få samma svar som när man använder uppgiftens koordinater. I kompendiet nämner de även att båda val av koordinater funkar.
Jag tror du har rätt när du säger att vinkeln mot insekten kan utgå från varsomhelst på ringen, jag har i min lösning sagt att den börjar gå vid $\phi$, men en förskjutning med en konstant vinkel borde väl ge samma svar..? Inte funderat på detta förrän nu, men jag tror det borde bli samma.
Min lösning följer i alla fall nedan, det finns lite kladd till höger på första sidan som inte är relevant. Med RMM menar jag rörelsemängdsmoment. Observera också att det fanns lite mer ledning än i mitt originalinlägg, exempelvis var en integral given. Ställ gärna fler frågor om du vill diskutera uppgiften mer eller om du undrar något när det gäller min lösning! :)
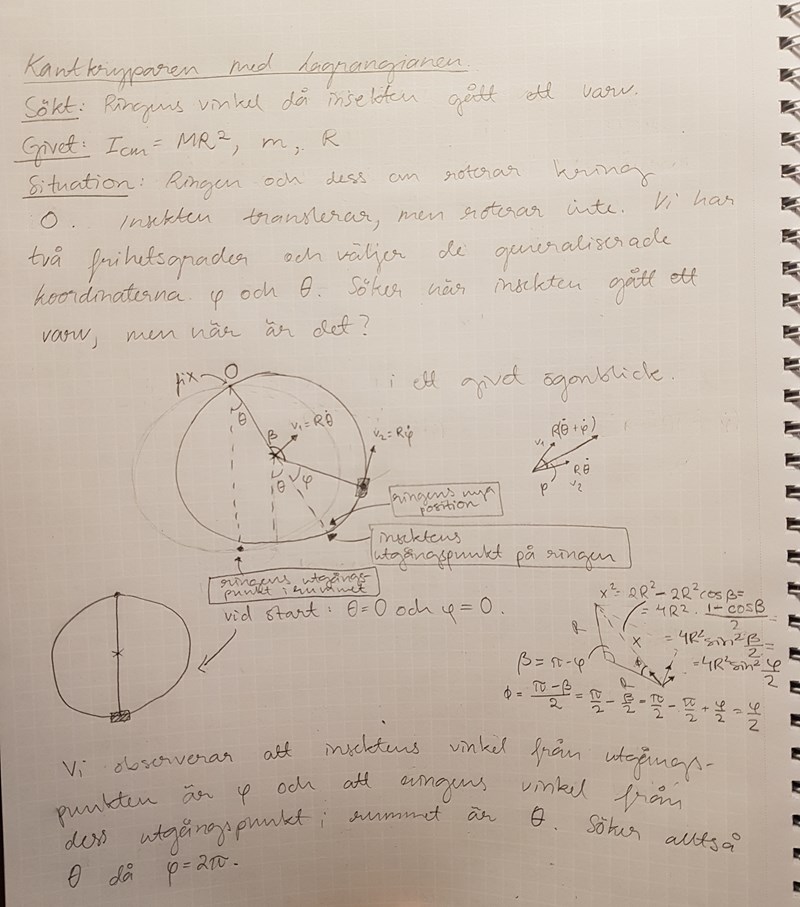

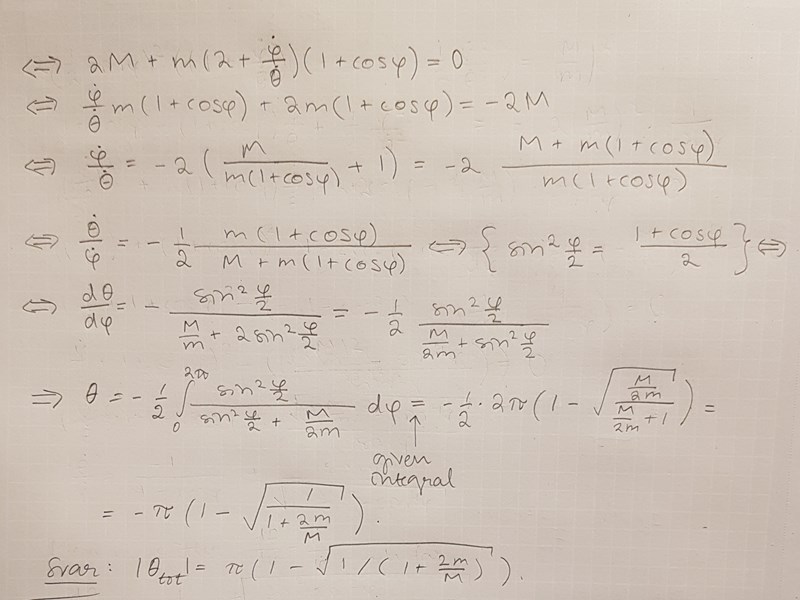
Väldigt snygg lösning! Jag gillar att du lägger vikt vid analysen och att du följer den klassiska sökt, givet-formuleringen. Framförallt att du använder skrivstil, det måste ges en eloge för.
Var antagandet du gjorde ett eget påfund? Att få fram ett analytiskt svar ser jag inte som möjligt utan det då differentialekvationen blir för komplicerad. Det blir väldigt smidigt när kraftmomentet från tyngdkrafterna försvinner och rörelsemängdsmomentet bevaras.
Tack så mycket! :) Jag har insett att en noggrann analys innan man påbörjar själva beräkningarna ger mindre utrymme för fel i resten av uppgiften.
Menar du antagandet att den ligger på ett bord? De kursansvariga nämnde att rörelsemängdsmomentet skulle bevaras, men eftersom det inte skulle bevaras om ringen låg i ett vertikalt plan antog jag att de missat att skriva att den låg horisontellt i uppgiften. Du har rätt i att det skulle bli för komplicerat om den låg vertikalt.



