Kluring - Bestäm a och gränsvärdet (Matematik/Allmänna diskussioner)

Den var räligare…

Luktar maclaurin-utveckling va? Känns som att man ska kunna välja a så att x^2-termerna i täljaren tar ut varandra för att sedan kunna bryta ut faktorn med minst grad (x^3) i täljare och nämnare och låta alla termer av högre grad gå mot noll.

Det förutsätter dock att konstant- och förstagradstermer också tar ut varandra när man utvecklar logaritmen. Och att andragradstermen från utvecklingen blir negativ.

Sen ser den ju lite halvjobbig ut att utveckla…

BUMP‼️ Någon som vågar sig på denna uppgift? 😉

Jag kan ju försöka. Av någon anledning så kommer jag att tänka på filmen "Dum, dummare dummast" när jag undrar vad ni kommer att tycka om mitt förslag, men här kommer det ändå.

För att få en uppfattning om vad som kommer att hända så provar vi med ett lågt värde, $x = 10^{- 10}$

$\lim_{x \to 0} a \frac{10^{- 20} + \ln (\sqrt{1 + 2 \cdot 10^{- 10}} - 10^{- 10})}{10^{- 30}}$ Uttrycket med ln kommer att gå mot ln(1)=0
Vi ser då att vi går mot 10^-20 / 10^-30 För att rädda situationen så sätter vi a=x och får 10^-30 / 10^-30

Så mitt förslag blir att a=x och gränsvärdet blir 1.

Du har a framför hela uttrycket, men i frågan står det bara framför x².

Laguna skrev:
Du har a framför hela uttrycket, men i frågan står det bara framför x².

Ja det var slarvigt av mig, men eftersom hela uttrycket med ln försvinner så blir det så på slutet.

Nej, detta var inte alls trivialt... Jag valde att utveckla med maclaurin som mitt sista försök, borde ha varit mitt första.

Visa spoiler

a=1/2 gör att gränsvärdet konvergerar till 1/2.

Jag kollade upp med GeoGebra och där ser man att Dracaenas svar ser rimligt ut.

Mitt fel var att underskatta ln-termen som inte alls gick mot noll så fort som jag trodde.

ln-termen längst ned på bilden, x³ i mitten och x² högst upp. Lägg märke till att x² är precis dubbelt så stor vid x=0,002 jämfört med ln-termen.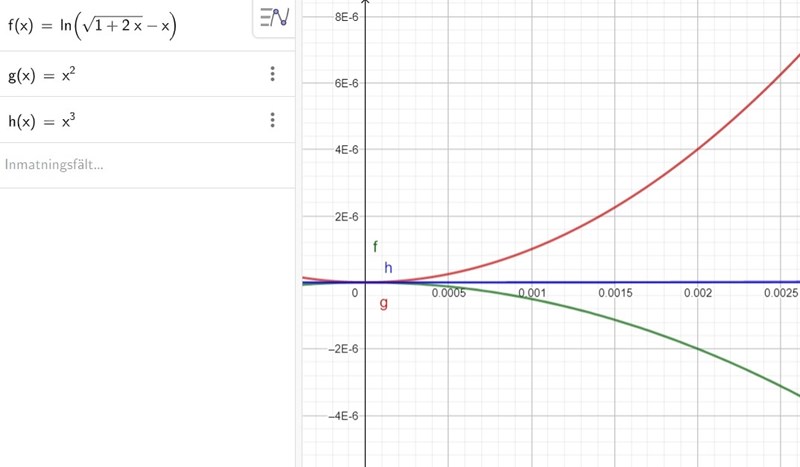

Är det mycket arbete att skriva ut maclaurin-utvecklingen? Det kunde vara intressant att se. Ännu har jag inte kommit dit i mina studier. Ja för 50 år sedan fick vi lära oss en maclaurin-formel i gymnasiet, men jag minns inte alla detaljer 😀

Maclaurin är egentligen bara Taylor vid $x = 0$ så att:

$f(x) = f(0) + x \dfrac{f^\prime (0)}{1!} +x^2 \dfrac{f^{\prime \prime} (0)}{2!}+....$

Jag räknade dessa för hand och stoppade sedan in i gränsvärdet och korrigerade $a$ så att gränsvärdet konvergerar. Det blir lite grisigt att derivera, men inte allt för jobbigt.

Jag gjorde en praktisk gränsvärdesberäkning med Python.

Dracaena skrev:
Det blir lite grisigt att derivera, men inte allt för jobbigt.

All ära till dig, jag tappade tålamodet efter andraderivatan (behöver tredje).

Men ja, med lite fusk från Wolfram Alpha's Taylor Series Calculator kom jag fram till samma svar som dig.

Alltså, $\ln (\sqrt{1 + 2 x} - x)$ kan skrivas om som $- \frac{x^{2}}{2} + \frac{x^{3}}{2} + x^{4} B (x)$ .

Då kan man skriva:

$\frac{a x^{2} + \ln (\sqrt{1 + 2 x} - x)}{x^{3}} = \frac{a x^{2} - \frac{x^{2}}{2} + \frac{x^{3}}{2} + x^{4} B (x)}{x^{3}}$

Visa spoiler

S ä t t a = \frac{1}{2} \Rightarrow \frac{\frac{x^{2}}{2} - \frac{x^{2}}{2} + \frac{x^{3}}{2} + x^{4} B (x)}{x^{3}} = \frac{\frac{x^{3}}{2} + x^{4} B (x)}{x^{3}} = \frac{x^{3}}{x^{3}} \frac{\frac{1}{2} + x B (x)}{1} = \frac{1}{2} + x B (x) \lim_{x \to 0} \frac{a x^{2} + \ln (\sqrt{1 + 2 x} - x)}{x^{3}} = \lim_{x \to 0} (\frac{1}{2} + x B (x)) = \frac{1}{2} + 0 = \frac{1}{2} a = \frac{1}{2} o c h g r ä n s v ä r d e t = \frac{1}{2}

Nu är det nog fler med mig som undrar hur ser din beräkning ut tomast80?

Jag har ju egentligen inte de bakgrundskunskaper som behövs, men jag jobbar med att komma längre i mitt matematiska kunnande. Därför skulle jag uppskatta mycket om du försöker att beskriva din tankegång på en nivå så att det kan ge oss nyfikna lite glädje av dina kluringar också.
jonnefcb har ju gjort en väldigt bra redogörelse för sin lösning så vitt jag förstår, men är det exakt så du också tänkt dig lösningen? Det brukar ju sällan bara finnas en väg till en lösning.

Hej!

Kan ge lite tips på vägen till att börja med. Ett sätt att lösa denna uppgift är Maclaurinutveckling i flera nivåer.

$(1+t)^b\approx 1+bt+\frac{bt^2}{2}+\frac{bt^3}{6}$

$\ln(1+z)\approx z-\frac{z^2}{2}+\frac{z^3}{3}$

Genom att sätta $t=2x$ , $b=\frac{1}{2}$ och $z=f(x)$ och förkasta högre ordningens termer kan man serieutveckla täljaren och sedan se till att andragradstermen blir $0$ genom ett lämpligt val av konstant $a$ .

tomast80 skrev:
Hej!

Kan ge lite tips på vägen till att börja med. Ett sätt att lösa denna uppgift är Maclaurinutveckling i flera nivåer.

$(1+t)^b\approx 1+bt+\frac{bt^2}{2}+\frac{bt^3}{6}$

$\ln(1+z)\approx z-\frac{z^2}{2}+\frac{z^3}{3}$

Genom att sätta $t=2x$ , $b=\frac{1}{2}$ och $z=f(x)$ och förkasta högre ordningens termer kan man serieutveckla täljaren och sedan se till att andragradstermen blir $0$ genom ett lämpligt val av konstant $a$ .

Tyvärr det där är ännu så länge helt obegripligt för mig, men det finns hopp. I min kurs så ingår detta i första terminen så det tar väl några år innan jag kommer dit 😀
Kanske att jag tjuvtittar lite på Jonas Månsson. Han har 11 delar om Maclaurinutveckling utlagda på YouTube.

tomast80 skrev:
Hej!

Kan ge lite tips på vägen till att börja med. Ett sätt att lösa denna uppgift är Maclaurinutveckling i flera nivåer.

$(1+t)^b\approx 1+bt+\frac{bt^2}{2}+\frac{bt^3}{6}$

$\ln(1+z)\approx z-\frac{z^2}{2}+\frac{z^3}{3}$

Genom att sätta $t=2x$ , $b=\frac{1}{2}$ och $z=f(x)$ och förkasta högre ordningens termer kan man serieutveckla täljaren och sedan se till att andragradstermen blir $0$ genom ett lämpligt val av konstant $a$ .

Den övre serieutvecklingen är fel, se formel nedan istället.

Här kommer, sent omsider, min lösning!