Kluring: en/ett-spel (Matematik/Allmänna diskussioner)

För någon som inte är så skarp på sannolikhet, avses här väntevärdet av slumpvariabeln som definieras enligt "antalet ord som dyker upp tills att samma ord har dykt upp två gånger, inklusive ordet som dyker upp igen"?

naytte skrev:
För någon som inte är så skarp på sannolikhet, avses här väntevärdet av slumpvariabeln som definieras enligt "antalet ord som dyker upp tills att samma ord har dykt upp två gånger, inklusive ordet som dyker upp igen"?

Hej! Korrekt uppfattat!

Hmm.

Bara några initiala tankar här.

Visa spoiler

Låt slumpvariabeln $X$ beteckna antalet ord vi ser tills två har dykt upp två gånger, inklusive ordet som dyker upp igen. De olika utfallen för $X$ är $x_1 = 2, x_2 = 3,..., x_{1000} = 1001$ . Enligt definitionen av väntevärde har vi då:

$\displaystyle \mu= \mathbb{E}\left(X\right)=\sum_{i}^{}x_i\mathbb{P}\left(X=x_i\right)$

Det kluriga nu är ju att sannolikheterna för varje utfall inte är lika stora. Det är uppenbart att det är betydligt mer sannolikt att det bara tar 20 försök än att det tar 1001 försök. När vi har lyckats bestämma ett lämpligt sannolikhetsmått för utfallen blir problemet rent aritmetiskt.

Visa spoiler

1001?

Mitt "?" då min tolkning av problemt är osäker.

Min privata teori här är att om det finns n tal att välja mellan så är förväntningen n+1.

En grej också, kan vi komma överens om att sätta svar i spoilers? Så att man inte spoilar problemet för varandra.

Jag vill minnas ett liknande problem från min gymn.tid som jag /typiskt/ inte kommer ihåg i detalj. Det handlade om hur man skulle uppskatta det totala antalet fiendetanks från de träffar man gjorde på ett fåtal. Det var hämtat från faktiska beräkningar under WWII, men jag kommer inte ihåg detaljerna. Det var en intressant problem. Någon som har stött på detta problem?

Jag slängde ihop ett script i Python för att få en känsla för fördelningen för olika antal ord samt för specialfallet då vi har 1000 ord, och jag måste säga att det är väldigt förvånande om det stämmer.

Kommentar + script + åskådliggöring för olika antal ord

Enligt mitt script ska väntevärdet vara endast ca. 40 ord. Det är förvånansvärt lågt. Jag vet inte om jag har gjort fel men jag bifogar min (slarviga!) kod om någon vill kolla. Jag bifogar också en åskådliggöring av hur väntevärdet ungefär ser ut för olika antal ord. Det ser nästan logaritmiskt ut:

Nedan följer scriptet:

import matplotlib.pyplot as plt
import random


def counter(words: list) -> int:
    seen = []
    x = 0
    while True:
        random_word = random.choice(words)
        if random_word in seen:
            x += 1
            return x

        else:
            seen.append(random_word)
            x += 1


def main() -> dict:
    words = []
    word_averages = {}

    for k in range(1000):
        x = 0
        words.append(f"{k}")

        for _ in range(1000):
            x += counter(words)

        word_averages[k] = (x / 1000)

    return word_averages


def main2():
    words = [f"{i}" for i in range(1000)]
    averages = []

    for _ in range(40):
        x = 0
        for _ in range(1000):
            x += counter(words)
        averages.append(x / 1000)

    print(averages)


def visualize(word_averages: dict):
    x = list(word_averages.keys())
    y = list(word_averages.values())

    plt.plot(x, y, marker='o')
    plt.xlabel('Antal ord')
    plt.ylabel('Approximerat väntevärde')
    plt.grid(True)
    plt.show()


if __name__ == "__main__":
    word_averages = main()
    visualize(word_averages)

naytte skrev:
Jag slängde ihop ett script i Python för att få en känsla för fördelningen för olika antal ord samt för specialfallet då vi har 1000 ord, och jag måste säga att det är väldigt förvånande om det stämmer.
Kommentar + script + åskådliggöring för olika antal ord

Enligt mitt script ska väntevärdet vara endast ca. 40 ord. Det är förvånansvärt lågt. Jag vet inte om jag har gjort fel men jag bifogar min (slarviga!) kod om någon vill kolla. Jag bifogar också en åskådliggöring av hur väntevärdet ungefär ser ut för olika antal ord. Det ser nästan logaritmiskt ut:

Nedan följer scriptet:
import matplotlib.pyplot as plt
import random


def counter(words: list) -> int:
    seen = []
    x = 0
    while True:
        random_word = random.choice(words)
        if random_word in seen:
            x += 1
            return x

        else:
            seen.append(random_word)
            x += 1


def main() -> dict:
    words = []
    word_averages = {}

    for k in range(1000):
        x = 0
        words.append(f"{k}")

        for _ in range(1000):
            x += counter(words)

        word_averages[k] = (x / 1000)

    return word_averages


def main2():
    words = [f"{i}" for i in range(1000)]
    averages = []

    for i in range(40):
        x = 0
        for _ in range(1000):
            x += counter(words)
        averages.append(x / 1000)

    print(averages)


def visualize(word_averages: dict):
    x = list(word_averages.keys())
    y = list(word_averages.values())

    plt.plot(x, y, marker='o')
    plt.xlabel('Antal ord')
    plt.ylabel('Approximerat väntevärde')
    plt.grid(True)
    plt.show()


if __name__ == "__main__":
    word_averages = main()
    visualize(word_averages)

Vad händer om du byter de n orden mot heltalen 1..n?

Menar du under main() där jag appendar "k" istället för k?

naytte skrev:
Menar du under main() där jag appendar "k" istället för k?

Jag tänkte att instället för att ta n olika ord så tar man talen 1..n. De är alla olika.

Om jag inte missförstår vad du menar så är det i princip redan det som händer. Heltalen läggs till som strängar och listan innehåller till slut strängarna ["1", "2", "3",..., "1000"]. Man hade väl kunnat lägga till dem som integers också egentligen, borde inte göra någon skillnad.

naytte skrev:
Om jag inte missförstår vad du menar så är det i princip redan det som händer. Heltalen läggs till som strängar och listan innehåller till slut strängarna ["1", "2", "3",..., "1000"]. Man hade väl kunnat lägga till dem som integers också egentligen, borde inte göra någon skillnad.

Det är jag som inte kan läsa Python...

Visa spoiler

Låt oss anta att vi har n tal, 1, 2, ..., n.

Slh att välja ett tal är 1 (hur kan man misslyckas). Vi kallar detta tal N.

Vi skall nu välja k-2 andra tal och sedan talet N igen.

Om vi antar att de är likafördelade och med p=1/n så blir

P(N=k)=1*(1-p)^(k-2)p

med v.v. SUM_2^inf k P(N=k) = n+1

Så var min tolkning.

@Trinity2:

Visa spoiler

Utgår du inte i din beräkning från att vi först väljer ett ord och sedan väntar på det ordet igen? Det kan väl hända att man får en sträng A[...]BCGG[...]A. I det här fallet "valde" vi A först men G dök upp två gånger innan det andra A:et dök upp.

naytte skrev:
@Trinity2:

Visa spoiler

Utgår du inte i din beräkning från att vi först väljer ett ord och sedan väntar på det ordet igen? Det kan väl hända att man får en sträng A[...]BCGG[...]A. I det här fallet "valde" vi A först men G dök upp två gånger innan det andra A:et dök upp.

Det är nog en mera korrekt tolkning av TS. Då kan nog dina värden vara rätt.

En liten tanke här bara:

Visa spoiler

Låt säga att vi har något passande sannolikhetsmått $\mathbb{P}$ . I så fall gäller det att:

$\displaystyle \mathbb{P}\left(\text{ingen upprepning på k försök}\right)=\frac{1000}{1000}\cdot\frac{999}{1000}\cdot...\cdot\frac{1000-(k-1)}{1000}=\prod_{k}\frac{1000-(k-1)}{1000}$

Så sannolikheten att vi får åtminstone en upprepning under $k$ försök måste vara:

$\displaystyle 1-\prod_{k}\frac{1000-(k-1)}{1000}$

Låt x_i vara ordet på position i

Så TS söker

min( { j : x_j=x_i } ), i<j.

?

Det känns som detta är ett "klassiskt" problem men jag vet inte dess namn. Kanske någon med gedigen matematisk historia vet.

Så TS söker

min( { j : x_j=x_i } ), i<j.

Medelvärdet av det uttrycket över extremt många iterationer, tolkar jag det som.

EDIT: jag läste det du skrev fel. Nej, jag tror inte det är detta som efterfrågas. Så som du formulerar det måste vi väl bestämma ett $i$ från början?

Relaterat(?) problem

Faktum är att nu när jag tänker efter så liknar detta problem the birthday problem ganska mycket. Men jag vet inte hur man löser det heller så det hjälper inte mig åtminstone, men kanske inspirerar det någon annan?

naytte skrev:

Så TS söker

min( { j : x_j=x_i } ), i<j.

Medelvärdet av det uttrycket över extremt många iterationer, tolkar jag det som.

EDIT: jag läste det du skrev fel. Nej, jag tror inte det är detta som efterfrågas. Så som du formulerar det måste vi väl bestämma ett $i$ från början?

Visa spoiler

Faktum är att nu när jag tänker efter så liknar detta problem the birthday problem ganska mycket. Men jag vet inte hur man löser det heller så det hjälper inte mig åtminstone, men kanske inspirerar det någon annan?

Jag tolkar det som:

Tag vilken sekvens av 1-bokstavs-"ord"

Börja på index 1 och finn när denna bokstav återkommer, säg på position j_1

Tag sedan index 2 och finn när denna bokstav återkommer, säg på position j_2

etc.

Vad är v.v. för j_k?

Men det kanske är fel tolkning. Det känns som ett (löpande) ffg-problem.

tomast80 kommer säkert med ett snyggt svar snart.

Jag tolkar det som att man bara helt enkelt slumpar fram orden och noterar hur många försök det tar tills något ord har förekommit två gånger. Om jag tolkar dig rätt så "glömmer" vi massor av försök när vi byter startindex.

Jag tror jag har en fullständig lösning nu, eller åtminstone ett "matematiskt svar" som jag inte vet hur man ska lösa för hand. Skulle @tomast80 kunna ge bekräftelse på om svaret är rätt, även om formen är praktiskt taget olösbar för hand?

Lösningsförslag

Jag tänkte vidare i samma bana som i #17 och insåg att vi ju faktiskt kan ta fram ett uttryck för sannolikheten att vi får upprepning på exakt det $k$ :te försöket. Låt $n$ beteckna antalet ord ( $n=1000$ i vårt fall):

$\displaystyle \mathbb{P}\left(X=k\right) = \underbrace{\frac{n}{n}\cdot \frac{n-1}{n}\cdot...}_{\text{$k-1$ }}\cdot\frac{k-1}{n}=\frac{k-1}{n}\prod_{i=0}^{k-2}\left(1-\frac{i}{n}\right)$

Så enligt definitionen av väntevärde har vi:

$\displaystyle \mathbb{E}\left(X\right)=\sum_{k=2}^{n+1}k\cdot\mathbb{P}\left(X=k\right)=\sum_{k=2}^{n+1}\frac{k\left(k-1\right)}{n}\prod_{i=0}^{k-2}\left(1-\frac{i}{n}\right)$

Mycket riktigt får vi enligt Wolfram Alpha:

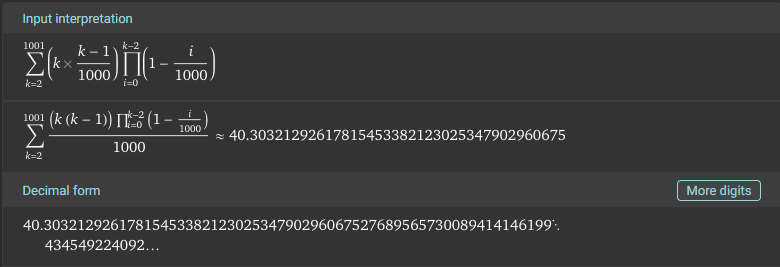
Men jag vet inte hur man ska göra utan att "fuska" med Wolfram Alpha. Visserligen är resonemanget matematiskt korrekt (hoppas jag, svaret verkar ju stämma i alla fall...) men det är nog hopplöst att försöka lösa den här summan för hand.

Hej! Tänkte faktiskt ut uppgiften lite spontant utifrån ett spel som jag konstruerade åt min dotter i Scratch, så har egentligen inget svar förberett, men kan bekräfta att naytte har rätt svar. Se från Gemini nedan. Skulle nog löst den på ett liknande sätt själv.

Jag gav upp efter 1 minut att läsa den USLA matematiska presentationen från "Gemini". Vad står här? Är det någon som menar allvar med denna text eller är det C/P-error?

Trinity2 skrev:
Jag gav upp efter 1 minut att läsa den USLA matematiska presentationen från "Gemini". Vad står här? Är det någon som menar allvar med denna text eller är det C/P-error?

Blev så när jag kopierade och klistrade in på Pluggakuten. Sparade som en bild nu i stället, blev det bättre?

tomast80 skrev:
Trinity2 skrev:
Jag gav upp efter 1 minut att läsa den USLA matematiska presentationen från "Gemini". Vad står här? Är det någon som menar allvar med denna text eller är det C/P-error?

Blev så när jag kopierade och klistrade in på Pluggakuten. Sparade som en bild nu i stället, blev det bättre?

Bara om man har falkögon.

Trinity2 skrev:
tomast80 skrev:
Trinity2 skrev:
Jag gav upp efter 1 minut att läsa den USLA matematiska presentationen från "Gemini". Vad står här? Är det någon som menar allvar med denna text eller är det C/P-error?

Blev så när jag kopierade och klistrade in på Pluggakuten. Sparade som en bild nu i stället, blev det bättre?

Bara om man har falkögon.

Jag provade igen nu med en större skärm, känns som det blev lite bättre.

Jag begriper ingenting av Geminis svar. Jag bekräftade med miniräknare att summan den föreslog faktiskt är lika med min summa. Det förefaller vara lite svartmagi haha. Menar du att du hade fört ett liknande resonemang som Gemini eller menar du att du hade gjort som jag, @tomast80?

naytte skrev:
Jag begriper ingenting av Geminis svar. Jag bekräftade med miniräknare att summan den föreslog faktiskt är lika med min summa. Det förefaller vara lite svartmagi haha. Menar du att du hade fört ett liknande resonemang som Gemini eller menar du att du hade gjort som jag, @tomast80?

I realiteten hade nog min lösning legat närmare din, Gemini krånglar till det onödigt mycket. Men i princip är det ju samma tänk bakom.