Kluring - kvadratens sida

Drag diagonalen $AD$, vilket skär $BC$ i punkt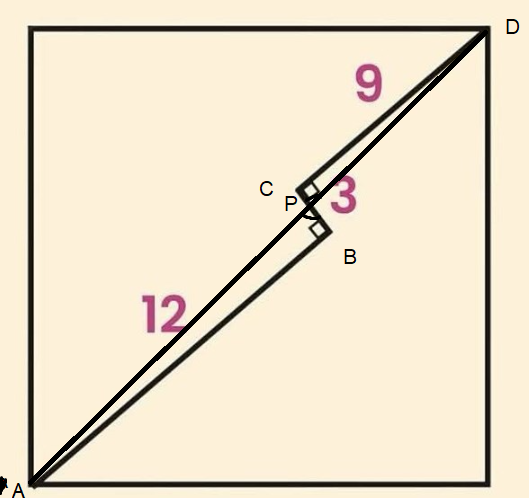en $P$:

De två räta linjerna som skär varandra i $P$ ger att $\angle APB = \angle DPC$ och då båda dessa trianglar har en rät vinkel följer det att de är likformiga, dvs $\triangle APB \sim \triangle DPC$. 

Likformigheten ger att

$\displaystyle \frac{|AP|}{|PD|} = \frac{|BP|}{|PC|} = \frac{12}9$

Vidare har vi att $|BP| + |PC| = 3$. Vi kan använda detta för att lösa ut $|BP| = 12/7$

Pythagoras ger att $\displaystyle \left|AP\right| = \sqrt{12^2 + \left(\frac {12}7\right)^2}=\frac{60}{7}\sqrt{2}$

Likformigheten ger att $|AD| = |AP| + |PD| = |AP| + \frac{3}4 |AP| = 15\sqrt{2}$

Låt sidlängden vara $s$. Pythagoras ger att $2s^2 = |AD|^2$, därmed har vi $s = 15$ le.

Parallellförflytta linjen med 9 så den blir en fortsättning på linjen med 12 vilket ger en triangel med basen 12+9=21 och höjden 3 där hypotenusan är diagonal osv.

Extrafråga: Vad är tan(a) där a är vinkeln mellan 12-linjen och horisontalplanet?