kodning i diskret matte
jag hade verkligen svårt att utföra denna uppgift. undrar om det finns någon här som kan hjälpa mig med det?
Dörren till sammanträdesrummet styrs av en boolesk krets, vars funktion ges av formeln f(x, y, z) =
x''y'(x '+ z).
12. Skriv om funktionens beräkningsformel till disjunktiv normalform med hjälp av räkneregler.
13. Gör upp en värdetabell för funktionen.
14. Rita kretsen. (Välj själv om du ska ta den ursprungliga eller den omräknade.)
mina Lösningar ( fel blev det )
12. ) Förenkla den booleska funktionen: f(x, y, z) = x''y'(x' + z).12 = (x')'(y')(x' + z).
(dubbel negation) = (x)(y')(x' + z).
(dubbel negation) = (x)(y')(x'z + z).
(distributiv lag)
Använd den distributiva lagen för att expandera uttrycket: f(x, y, z) = (xy'x' + xyz).
(distributiv lag) = (0 + xyz).12 (komplementlag) = xyz.12 (0 + a = a)
Skriv om uttrycket i DNF: f(x, y, z) = (x' + y + z')(x + y' + z)(x + y + z).
.jpg?width=800&upscale=false)
Hej och välkommen på pluggakuten!
Ja, det finns några problem med din lösning.
Först och främst ser en disjunktiv normalform ut så här: (abc)+(de)+(fg) dvs "en summa av produkter" och inte "en produkt av summor".
Ditt första steg är okej:
12. ) Förenkla den booleska funktionen: f(x, y, z) = x''y'(x' + z).12 = (x')'(y')(x' + z).
(dubbel negation) = (x)(y')(x' + z).
Det är bra, men här kan du direkt tillämpa den distributiva lagen:
xy'(x'+z) = xy'x' + xy'z
(associativa och kommutativa lagar)
xy'x' + xy'z = (xx')y' + xy'z
(a*a'= 0)
(xx')y' + xy'z = 0y' + xy'z
(domination och additiv identitet)
0y' + xy'z = xy'z
tack så jätte mycket för hjälpen !
undrar om det går att lösa fråga 13 och 14 om någon kan lösa den ?
faisal98 skrev:tack så jätte mycket för hjälpen !
undrar om det går att lösa fråga 13 och 14 om någon kan lösa den ?
BEHÖVER AKUT HJÄLP!!!!
uppgift 13 och 14
Jätte tacksam om någon svara!
Gör en tabell för fråga 13. Ditt första försök stämde ju inte.
xy'z = 1 om (x=1 och y=0 och z=1)
Det är svårt att rita kretsen utan att veta vilka komponenter du får välja.
Jag antar att du får använda grindar och behöver inte bygga upp kretsen från transistorer.
Två möjliga lösningar: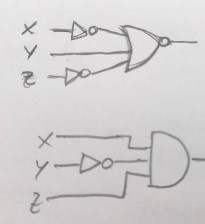
Macilaci skrev:Det är svårt att rita kretsen utan att veta vilka komponenter du får välja.
Jag antar att du får använda grindar och behöver inte bygga upp kretsen från transistorer.
Två möjliga lösningar:
Tackar er alla för eran hjälp
Undrar bara om tabellen är rätt så som jag har gjord de?
Här är en värdetabell för den förenklade booleska funktionen f(x, y, z) = xy'z:
| x | y | z | f(x,y,z) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
Ja, den tabellen stämmer.
Laguna skrev:Ja, den tabellen stämmer.
Detta kommentarerna jag har fått om lösningarna från min lektions lärare
"Första steget i uppgift 12 är felaktigt, och det gör att allt efter det behöver göras om. Med den notation du har nu ska formeln skrivas
och första beräkningssteget ska vara De Morgans lag:
Det kommer att bli fler termer i den disjunktiva normalformen, fler rader med värdet 1, och en mycket krångligare krets."
Var det några formler i den texten också? De försvann.
Laguna skrev:Var det några formler i den texten också? De försvann.
ja det ska stå så här:
"Första steget i uppgift 12 är felaktigt, och det gör att allt efter det behöver göras om. Med den notation du har nu ska formeln skrivas f(x,y,z)= (x'y)' (x' + z)
och första beräkningssteget ska vara De Morgans lag: = (x''+y') (x' + z)
Det kommer att bli fler termer i den disjunktiva normalformen, fler rader med värdet 1, och en mycket krångligare krets."
Jag förstår inte allt det där. Tabellen påverkas inte alls av hur man skriver om funktionen. Med den givna f är det bara 1 på en enda rad.
Macilaci skrev:Hej och välkommen på pluggakuten!
Ja, det finns några problem med din lösning.
Först och främst ser en disjunktiv normalform ut så här: (abc)+(de)+(fg) dvs "en summa av produkter" och inte "en produkt av summor".
Ditt första steg är okej:
12. ) Förenkla den booleska funktionen: f(x, y, z) = x''y'(x' + z).12 = (x')'(y')(x' + z).
(dubbel negation) = (x)(y')(x' + z).
Det är bra, men här kan du direkt tillämpa den distributiva lagen:
xy'(x'+z) = xy'x' + xy'z
(associativa och kommutativa lagar)
xy'x' + xy'z = (xx')y' + xy'z
(a*a'= 0)
(xx')y' + xy'z = 0y' + xy'z
(domination och additiv identitet)
0y' + xy'z = xy'z
"Första steget i uppgift 12 är felaktigt, och det gör att allt efter det behöver göras om. Med den notation du har nu ska formeln skrivas f(x,y,z)= (x'y)' (x' + z)
och första beräkningssteget ska vara De Morgans lag: = (x''+y') (x' + z)
Det kommer att bli fler termer i den disjunktiva normalformen, fler rader med värdet 1, och en mycket krångligare krets."
Kan du ta en bild på uppgiftstexten?
Aha. Det som står är inte samma som det du skrev.
Och jag ser ytterligare ett problem: uppgiften nämnar den disjunktiva normalformen som är (ab)+(cd)
(se t.ex. här: https://sv.wikipedia.org/wiki/Normalform_(logik) )
()
Men läraren förväntar sig tydligen något i stil med (a+b)(c+d), som är den konjunktiva normalformen.
Tabellen kan se ut så här:
| x | y | z | x+y' | x'+z | (x+y')(x'+z) |
| 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Macilaci skrev:Och jag ser ytterligare ett problem: uppgiften nämnar den disjunktiva normalformen som är (ab)+(cd)
(se t.ex. här: https://sv.wikipedia.org/wiki/Normalform_(logik) )
()
Men läraren förväntar sig tydligen något i stil med (a+b)(c+d), som är den konjunktiva normalformen.
jag har gjord samma som du nämner nu i tidigare försök, men ändå räknades de inte!
kan du visa det sättet du menar att läraren vill att det ska vara?
tack så jätte mycket
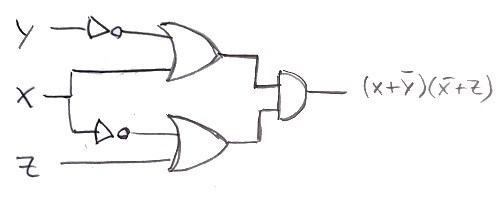
Om du är ute efter konjunktiva normalformen:
(deMorgan, som läraren skrev)
(x'y)'(x'+z) = (x+y')(x'+z)
Och det är vad du ser i min tabell.
faisal98 skrev:
det sägs ju här på fråga 12 att man ska skriv om det till disjunktiv normalform
Här är ett exempel som jag försökte men inte gick så bra
Jag tror inte läraren vill ha konjunktiv normalform, utan att det som den syftar på bara är första steget mot disjunktiv normalform.
Laguna skrev:Jag tror inte läraren vill ha konjunktiv normalform, utan att det som den syftar på bara är första steget mot disjunktiv normalform.
Kan du snälla visa hur man kan göra just min uppgift i de beräkningstegen ?
Okej, vi börjar, som läraren sa, med deMorgan:
(x'y)'(x'+z) = (x+y')(x'+z)
Nu kan du använda den distributiva lagen:
(x+y')(x'+z) = xx' + xz + y'x' + y'z
Komplementlag (aa' = 0) och additiv identitetselement (0+a = a):
xx' + xz + y'x' + y'z = 0 + xz + y'x' + y'z = xz + y'x' + y'z
Nu utökar vi varje term så att de innehåller alla variabler (t.ex. xz = xzy + xzy'):
(Här utnyttjar vi det multiplikativa identitetselementet, komplementlagen och distributiva lagen.)
xz + y'x' + y'z = xzy + xzy' + y'x'z + y'x'z' + y'zx + y'zx'
Associativitet (multiplikation):
xzy + xzy' + y'x'z + y'x'z' + y'zx + y'zx' = xyz + xy'z + x'y'z + x'y'z' + xy'z + x'y'z
Associativitet (addition):
xyz + xy'z + x'y'z + x'y'z' + xy'z + x'y'z = xyz + xy'z + xy'z + x'y'z + x'y'z + x'y'z'
Idempotens:
xyz + (xy'z + xy'z) + (x'y'z + x'y'z) + x'y'z' = xyz + xy'z + x'y'z + x'y'z'
Macilaci skrev:Okej, vi börjar, som läraren sa, med deMorgan:
(x'y)'(x'+z) = (x+y')(x'+z)
Nu kan du använda den distributiva lagen:
(x+y')(x'+z) = xx' + xz + y'x' + y'z
Komplementlag (aa' = 0) och additiv identitetselement (0+a = a):
xx' + xz + y'x' + y'z = 0 + xz + y'x' + y'z = xz + y'x' + y'z
Nu utökar vi varje term så att de innehåller alla variabler (t.ex. xz = xzy + xzy'):
(Här utnyttjar vi det multiplikativa identitetselementet, komplementlagen och distributiva lagen.)
xz + y'x' + y'z = xzy + xzy' + y'x'z + y'x'z' + y'zx + y'zx'
Associativitet (multiplikation):
xzy + xzy' + y'x'z + y'x'z' + y'zx + y'zx' = xyz + xy'z + x'y'z + x'y'z' + xy'z + x'y'z
Associativitet (addition):
xyz + xy'z + x'y'z + x'y'z' + xy'z + x'y'z = xyz + xy'z + xy'z + x'y'z + x'y'z + x'y'z'
Idempotens:
xyz + (xy'z + xy'z) + (x'y'z + x'y'z) + x'y'z' = xyz + xy'z + x'y'z + x'y'z'
tack så jättemycket för hjälpen 🙏🏾
nu när vi har fått annorlunda resultat ska man inte ändra på uppgift 13 och 14 ?
Macilaci skrev:Tabellen kan se ut så här:
x y z x+y' x'+z (x+y')(x'+z) 0 0 0 1 1 1 0 0 1 1 1 1 0 1 0 0 1 0 0 1 1 0 1 0 1 0 0 1 0 0 1 0 1 1 1 1 1 1 0 1 0 0 1 1 1 1 1 1
Den högra spalten i tabellen förblir densamma, men du kan glömma spalterna x+y' och x'+z (Jag skapade dem bara för att hjälpa till att beräkna resultatet. Men nu får du resultatet direkt från x, y och z).
Kretsen för det ursprungliga uttrycket är enklast: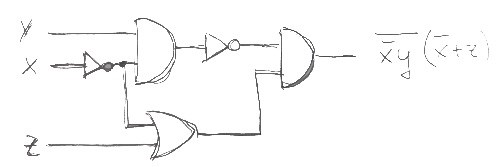
Macilaci skrev:Macilaci skrev:Tabellen kan se ut så här:
x y z x+y' x'+z (x+y')(x'+z) 0 0 0 1 1 1 0 0 1 1 1 1 0 1 0 0 1 0 0 1 1 0 1 0 1 0 0 1 0 0 1 0 1 1 1 1 1 1 0 1 0 0 1 1 1 1 1 1 Den högra spalten i tabellen förblir densamma, men du kan glömma spalterna x+y' och x'+z (Jag skapade dem bara för att hjälpa till att beräkna resultatet. Men nu får du resultatet direkt från x, y och z).
Kretsen för det ursprungliga uttrycket är enklast:
Tack så hemskt mycket för för hjälpen. Ska få se nu vad läraren kommer att kommentera om det.
För att skriva om funktionen f(x, y, z) till disjunktiv normalform (DNF) använder vi reglerna för boolesk algebra:
f(x, y, z) = (x')(y')(x' + z)
Första steget är att applicera dubbel negation:
f(x, y, z) = (x)(y')(x' + z)
Därefter använder vi den distributiva lagen för att expandera uttrycket:
f(x, y, z) = (xy'x' + xyz)
Nu kan vi förenkla uttrycket genom att använda komplementlagen:
f(x, y, z) = (0 + xyz)
Slutligen kan vi skriva om uttrycket i disjunktiv normalform:
f(x, y, z) = xyz
För att göra upp en värdetabell för funktionen f(x, y, z) = xyz, behöver vi lista alla kombinationer av x, y och z och bestämma värdet för f i varje kombination. Här är värdetabellen: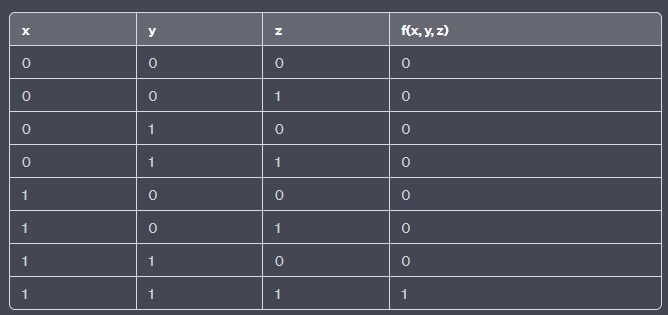
För att rita kretsen för funktionen f(x, y, z) = xyz, behöver vi använda booleska grindar. Eftersom f(x, y, z) = xyz, behöver vi en AND-grind för varje kombination av x, y och z.
En möjlig representation av kretsen kan se ut så här:
lua
________
x ---->| |
| AND |---- f
y ---->|______|
________
z ---->| |
| AND |
|______|
Denna krets består av tre AND-grindar, en för varje kombination av x, y och z. Grindarna är kopplade så att utgången från varje AND-grind är kopplad till nästa AND-grind, och slutligen är utgången från den sista AND-grinden utgången för hela kretsen, f(x, y, z).
fafen skrev:För att skriva om funktionen f(x, y, z) till disjunktiv normalform (DNF) använder vi reglerna för boolesk algebra:
f(x, y, z) = (x')(y')(x' + z)
Som framgår av inlägg #16 var detta INTE den funktion som uppgiften egentligen handlade om.




-felix-af-jochnick---linkedin.jpg?width=80&crop=0,0,80,80)
