Kolla över härledning av analysens fundamentalsats - infinitesimaler

God kväll!

Jag sitter och försöker få till integrering med infinitesimaler. Just nu har jag en fungerande definition för vad integraloperatorn betyder, men bestämda integraler har jag inte ännu. Jag har däremot definierat:

$\displaystyle \int_{t=a}^{t=b}f(t)\mathrm{d}t:=F(b)-F(a)$

Det jag vill visa är att arean mellan en godtycklig, kontinuerlig kurva $y=f(t)$ och x-axeln över något stängt intervall $[a,b]$ är samma sak som att beräkna integralen ovan. Det känns som om jag är nära, men jag lyckas inte färdigställa det. Antag att vi har en funktion $A(b)$, som ger arean mellan $t=0$ och $t=b$. Antag sedan att gör en infinitesimal förflyttning $\Delta t$. Se bild nedan:

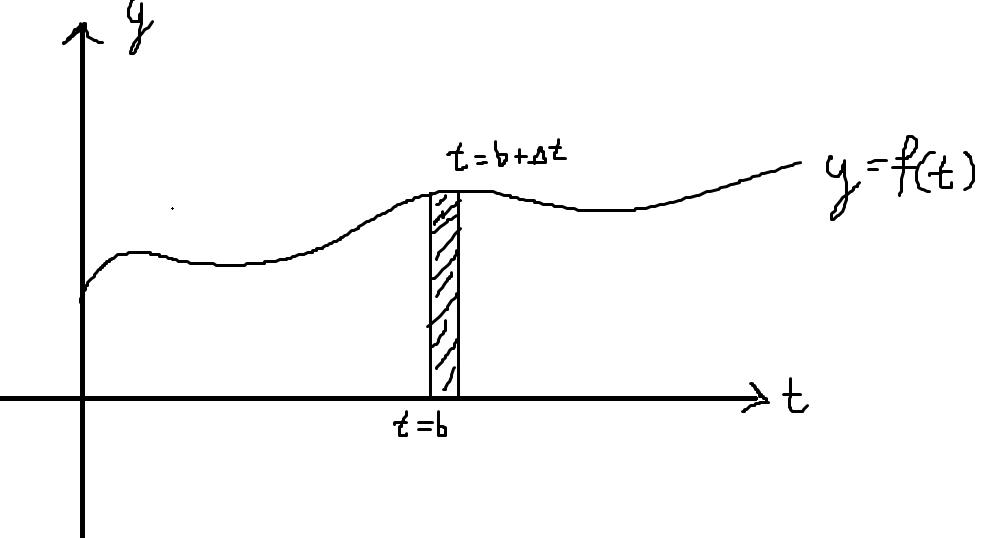
Arean på det ifyllda området kan vi då skriva som $\displaystyle A(b+\Delta t)-A(b)$. Vi vet dessutom att vi för någon passande infinitesimal $\beta$ kan uttrycka arean som $\displaystyle \Delta t(f(b)+\beta)$. Vi får alltså följande likhet:

$\displaystyle A(b+\Delta t)-A(b)=\Delta t(f(b)+\beta) \iff \frac{A(b+\Delta t)-A(t)}{\Delta t}=f(b)+\beta$

Nu tar vi realdel på båda sidor och erhåller:

$\displaystyle \mathrm{Re}\frac{A(b+\Delta t)-A(t)}{\Delta t}=\mathrm{Re}(f(b)+\beta)\iff A'(b)=f(b)$

Detta ger oss slutligen $\displaystyle \mathrm{d}A=f(t)\mathrm{d}t\iff A(b)=F(b)+C$

Sedan tänker jag att man gör samma sak fast för den undre gränsen $a$. Sedan ser man lätt att området på intervallet $[a,b]$ måste vara $F(b)-F(a)$, dvs följande integral:

$\displaystyle \int_{t=a}^{t=b}f(t)\mathrm{d}t$

---

Detta känns rätt, men jag vill bara bekräfta att det är rätt också.