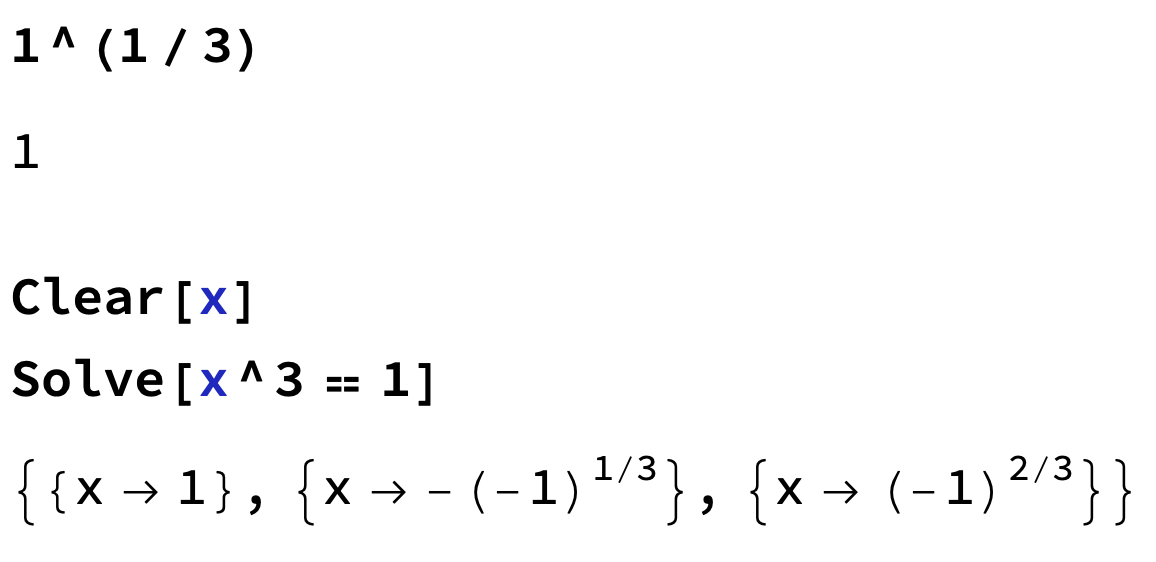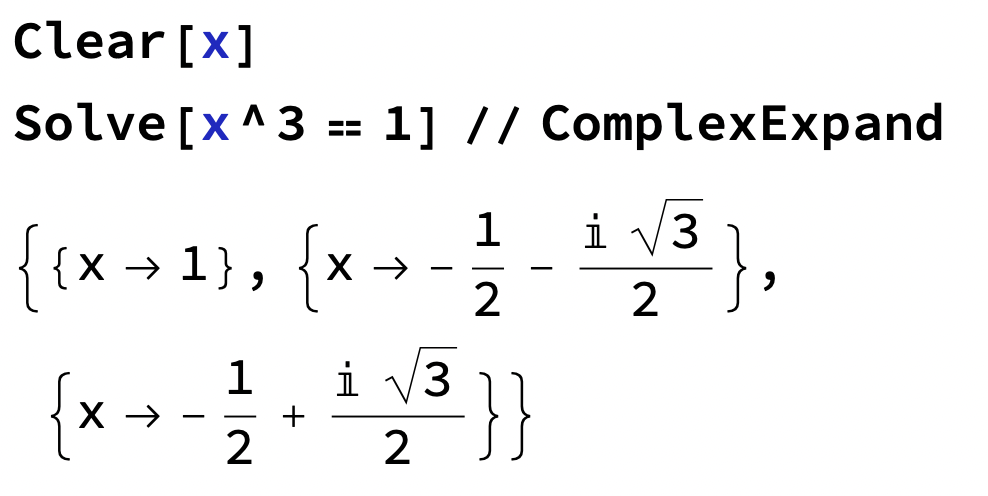Komplex analys - är det korrekt att säga att tredje roten ur 1 har tre värden?

naytte skrev:

Halloj!

Jag håller på att ta ikapp en kurs i komplex analys efter en del slappande och kollar nu på en videoserie som behandlar dess grunder. I en av videorna påstår föreläsaren i princip att $\displaystyle \sqrt[3]{1}$ skulle ha tre värden. Kan detta verkligen stämma? $\sqrt[3]{1}$ borde väl vara ett tal och således bara ha ett värde. Jag kan köpa att ekvationen

$\displaystyle x^3=1$

har tre lösningar i $\mathbb{C}$, men det kan väl inte vara så att $\sqrt[3]{1}$ har tre värden samtidigt? Jag misstänker att detta är lite begreppsslarv från föreläsarens sida på samma sätt som vissa säger att $\sqrt{9}$ skulle ha två värden när det egentligen bara motsvarar ett tal.

Nej, en operator har endast ett värde (givet dess värdemängd)

rot(9)=3

rot(49)=7

3-rot(27)=3

etc.

Ekvationer däremot kan ha många lösningar givet en talmängd (t.ex. N, Z, C)

Exempel (Mathematica)

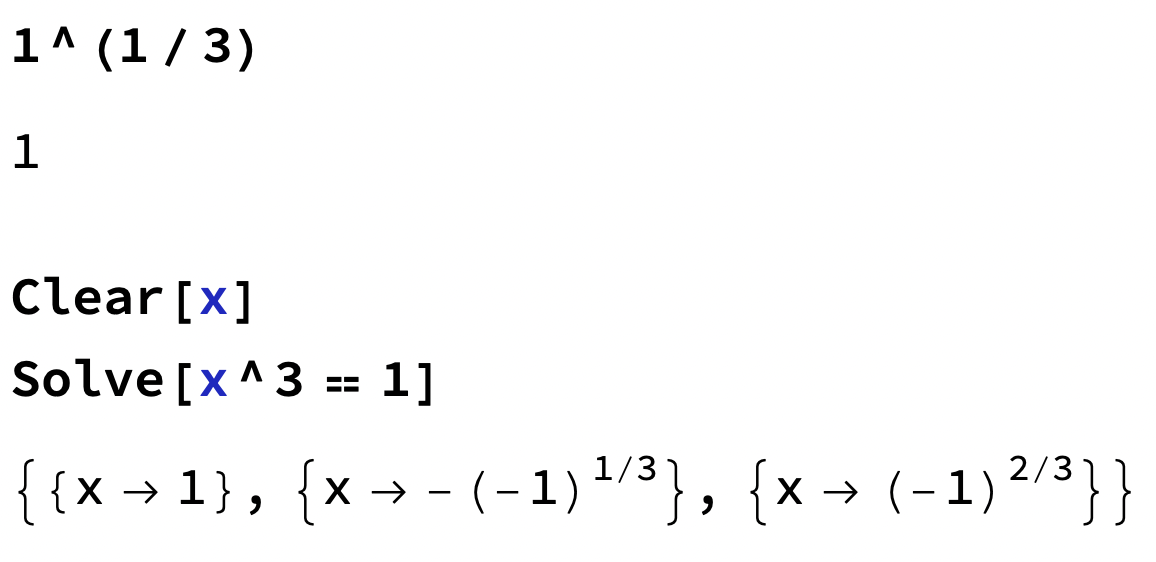
Det sista är lite kryptiskt, så vi utvecklar det komplext;

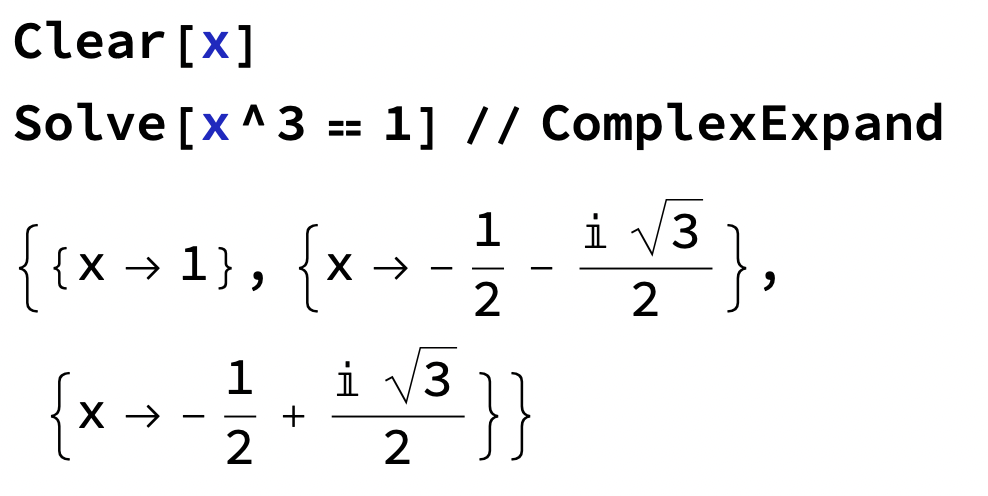
Precis, så det är alltså föreläsaren som uttrycker sig lite förvirrat?

naytte skrev:

Precis, så det är alltså föreläsaren som uttrycker sig lite förvirrat?

Ja, jag skulle gissa på att denne tänker rätt men kanske inspelningen gör denne nervös och tungan går sin egen väg ifrån hjärnan.

Okej, fint! Jag misstänkte detta men jag ville bara få det bekräftat. Apropå detta kom jag att tänka på den här memen:

Tycker den är väldigt lustig!

naytte skrev:

Okej, fint! Jag misstänkte detta men jag ville bara få det bekräftat. Apropå detta kom jag att tänka på den här memen:

Tycker den är väldigt lustig!

:) 

Stackars Julia har fått bli poster girl för populasens inställning till matematik...

Inte utan att man har haft samma blick ett par gånger i livet...

Det är inte helt ovanligt att man pratar om "flervärda" funktioner inom komplex analys. Till exempel insisterade användaren HenrikE (en matematiker som jag väldigt mycket såg upp till och som tyvärr gick bort för några år sedan) på det språkbruket i en tråd på gamla PA.

Jag är inget stort fan av att uttrycka sig så, dels eftersom det är svårt att formalisera det mängdteoretiskt och dels eftersom det lätt skapar förvirring i undervisningssituationer.

Är $(\left(-1\right)\cdot\left(-1\right))^\frac12$ samma sak som $(-1)^\frac12 \cdot (-1)^\frac12$?

Varför/varför inte?

D4NIEL skrev:

Är $(\left(-1\right)\cdot\left(-1\right))^\frac12$ samma sak som $(-1)^\frac12 \cdot (-1)^\frac12$?

Varför/varför inte?

Min digitala kompis säger

Det finns faktiskt förutsättningar under vilka $(z_1z_2)^c = z_1^c\cdot z_2^c$ även för komplexa tal, men för att förstå hur vi hamnade på olika grenar ovan måste vi först erkänna att det inte bara är principalvärden och/eller principalgrenar som påverkas av vårt grenval (val av branch cut). Ett annat klassiskt exempel är integralen $\int_\gamma z^{-\frac12}\,\,\mathrm{d}z$ där $\gamma$ är en cirkel runt origo. Om man klamrar sig fast vid ett "entydigt" principalvärde på $z^{-\frac12}$ borde integralen runt en sluten bana vara noll (som för en vanlig analytisk funktion utan singularitet).

D4NIEL skrev:

Det finns faktiskt förutsättningar under vilka $(z_1z_2)^c = z_1^c\cdot z_2^c$ även för komplexa tal, men för att förstå hur vi hamnade på olika grenar ovan måste vi först erkänna att det inte bara är principalvärden och/eller principalgrenar som påverkas av vårt grenval (val av branch cut). Ett annat klassiskt exempel är integralen $\int_\gamma z^{-\frac12}\,\,\mathrm{d}z$ där $\gamma$ är en cirkel runt origo. Om man klamrar sig fast vid ett "entydigt" principalvärde på $z^{-\frac12}$ borde integralen runt en sluten bana vara noll (som för en vanlig analytisk funktion utan singularitet).

Det var 6000 år sedan jag läste komplex analys m.m. så jag förstår ej mycket av din text. Matematik ligger kanske för nära filosofi för sitt eget bästa?

Mja, att reda ut under vilka förutsättningar potenslagen

$(z_1z_2)^c=z_1^c\cdot z_2^c$

gäller tycker jag ändå känns som en ganska konkret fråga när man börjar fundera vad vilka poänger konceptet "multivalued" egentligen kan tänkas ha :-)

Trinity2 skrev:

naytte skrev:

Halloj!

Jag håller på att ta ikapp en kurs i komplex analys efter en del slappande och kollar nu på en videoserie som behandlar dess grunder. I en av videorna påstår föreläsaren i princip att $\displaystyle \sqrt[3]{1}$ skulle ha tre värden. Kan detta verkligen stämma? $\sqrt[3]{1}$ borde väl vara ett tal och således bara ha ett värde. Jag kan köpa att ekvationen

$\displaystyle x^3=1$

har tre lösningar i $\mathbb{C}$, men det kan väl inte vara så att $\sqrt[3]{1}$ har tre värden samtidigt? Jag misstänker att detta är lite begreppsslarv från föreläsarens sida på samma sätt som vissa säger att $\sqrt{9}$ skulle ha två värden när det egentligen bara motsvarar ett tal.

Nej, en operator har endast ett värde (givet dess värdemängd)

rot(9)=3

rot(49)=7

3-rot(27)=3

etc.

Ekvationer däremot kan ha många lösningar givet en talmängd (t.ex. N, Z, C)

Exempel (Mathematica)

Det sista är lite kryptiskt, så vi utvecklar det komplext;

Ang D4niels andra inlägg. Kan z^-1/2 sakna singularitet i origo?

Okej, så i komplex analys börjar vi alltså tala om funktioner som är "flervärda"? Jag trodde att definitionen av att en mängd är en funktion är just att den inte är flervärd, alltså ska en mängd $f$ uppfylla kriteriet nedan för att vara en funktion

$\displaystyle (x,y_1),(x,y_2)\in f\implies y_1=y_2$ 

Har vi en ny definition i komplex analys eller missförstår jag diskussionerna?

Nu när jag kollar vidare definierar han nämligen begreppet analytisk som

A function $f\left(z\right)$ is analytic in a domain $\displaystyle \mathcal{D}\subseteq \mathbb{C}$ if $\displaystyle f\left(z\right)$ is single valued and has a finite derivative $\displaystyle f^\prime\left(z\right)$ for every $z\in\mathcal{D}$

Så vi verkar alltså ha svävat bort lite från den "vanliga" definitionen av funktion.

Ja, en flervärd funktion $f:X\to Y$ kan formellt sett ses som endast en delmängd av $X\times Y$, utan något speciellt krav att $(x,y_1),(x,y_2)\in f\implies y_1=y_2$. Det är alltså absolut inte en funktion, och för att särskilja dem kan man kalla vanliga funktioner för "envärda" funktioner. En flervärd funktion kan ofta göras till en envärd funktion genom att man väljer några principiella värden längs någon av funktionens "grenar" (till exempel att vi alltid väljer den positiva kvadratroten för positiva reella tal).

Okej, så att kalla "en flervärd funktion" för "funktion" är lite att missbruka begreppet funktion? Det vill säga, en flervärd funktion är inte en "funktion" utan just en "flervärd funktion"; "flervärd funktion" som sammansatt begrepp innebär alltså inte att objektet i fråga är en funktion?

Tillägg: 5 okt 2025 14:09

Väldigt pratigt inlägg men jag hoppas att frågan framgår.

Ja, det är lite olycklig terminologi eftersom det inte är en funktion i den vanliga bemärkelsen, därav nödvändigheten av begreppet "envärd funktion" för att specificera vad man menar. Det finns ju dock andra sorters snarlika begrepp som inte riktigt är vanliga funktioner men är liknande på andra sätt, t.ex. partiella funktioner (där man tillåter "funktionen" $f:X\to Y$ att vara odefinierad för vissa $x\in X$).

Vilken definition av "funktionen" $\log(z)$ använder ni i kursen?

Den vanligaste definitionen är förmodligen

$\log(z)=\ln r + i\theta, \quad r> 0$

där funktionen är flervärd (wikipedia). Sedan definieras principalvärdet som restriktionen (nu med stort L)

$\mathrm{Log}(z)=\mathrm{Log}(r)+i\theta,\quad r>0,\quad -\pi<\theta\leq \pi$

Notera särskilt var olikheten är sträng.

Och slutligen är  principalgrenen ungefär samma sak som principalvärdet förutom att logaritmen som analytisk funktion saknar värde för negativa reella tal (dvs då $\theta=\pi$). Det innebär att vi godtyckligt skurit bort $y=0,\, x\leq0$ om vi ser det komplexa talplanet som ett $xy$-plan. Vi kan naturligtvis skapa andra godtyckliga områden $D$ där logaritmen är analytisk och olika författare har olika uppfattningar om vad såväl principalvärde som principalgrenen ska vara, men detta torde vara de vanligaste.

Jag tror att vi definierade den flervärda komplexa logaritmen med hjälp av det principala argumentet för $z$, dvs.

$\displaystyle \mathrm{log}\left(z\right)=\ln r + i\left(\arg\left(z\right)+2\pi n\right)$

där $r>0$ och såklart $-\pi < \arg\left(z\right)\le \pi$

och sedan principalgrenen på samma sätt som du visade, alltså då $n=0$.

Symbolen $a^b$ där $a$ och $b$ är godtyckliga komplexa tal ($a\neq 0$) brukar definieras som $\displaystyle e^{b\log(a)}$. Eftersom den komplexa logaritmen $\log(a)$ är flervärd i bemärkelsen

$\log(a)=\ln|a| +i(\arg(a)+2\pi n),\quad n\in\mathbb{Z}$

blir även $a^b$ en flervärd funktion:

$\displaystyle a^b=e^{b(\ln|a|+i(\arg a +2\pi n) )}$

De olika värdena skiljer sig åt med faktorn $e^{2\pi bni}$. För $a>0$ (ett reellt tal större än noll) reducerar $a^b$ till ett entydigt värde. Låter vi dessutom $b$ vara ett heltal kan vi tolka symbolen som antingen $a$ eller $a^{-1}$. Om slutligen $b$ är ett rationellt tal $p/q$ (bråket förenklat så långt som möjligt) antar $a^b$ exakt $q$ olika värden och kan uttryckas som $\sqrt[q]{a^p}$ .

Jag håller med dig om att en funktion borde vara entydig. Bara det faktum att vi måste använda pleonasmer som "envärdig" för att särskilja de flervärda funktionerna $\sqrt{z}$ och $\log(z)$ från "riktiga" funktioner visar att något är skumt. Men under särskilt gynnsamma omständigheter kan man alltså välja sin branch så att funktionerna i ett visst område blir envärda. Detta räcker för det mesta för att tillfredsställa behovet av matematisk ordning och reda. Men till skillnad från det reella fallet (där vi låter $\sqrt{9}=3$) kan vi inte bara välja en gren "för alltid" och gå vidare.

Hur man ska behandla problemet med flervärdigheten är ett väldigt spännande kaninhål. Ett sätt är att "lappa ihop" ett antal funktionselement till kedja

$(f_1,\Omega_1), (f_2,\Omega_2),\dots$

där varje $(f_{k+1},\Omega_{k+1})$ är direkt analytisk fortsättning på den förgående $(f_k, \Omega_k$). Den ekvivalensklass som bildas av alla sådana kedjor är globalt analytisk, och kan representeras som en envärd analytisk funktion på en Riemannyta. Skulle dock råda dig att utforska det här först det när tentorna är över om du redan ligger lite efter i grundkursen :-)

Slutligen angående din ursprungliga fråga; eftersom $a=1$ och $b=p/q=1/3$ i ditt uttryck antar $1^{1/3}$ exakt 3 värden och det är det jag tror föreläsaren vill illustrera.

Tack för ditt utförliga svar!

Jag blir lite fundersam kring detta:

De olika värdena skiljer sig åt med faktorn $e^{2\pi b ni}$ För $a>0$ (ett reellt tal större än noll) reducerar $a^b$ till ett entydigt värde.

Jag förstår inte riktigt vad du menar med detta. Då $a=1>0$ och $b=1/3$ reduceras väl $a^b$ inte till ett entydigt värde?

Men om vi tar $1^{1/3}$ som konkret exempel borde vi alltså ha

$\displaystyle \left(1\right)^{1/3}=e^{\frac{1}{3}\left(\ln|1|+i(\mathrm{Arg}(1)+2\pi n)\right)}=e^{\frac{2\pi n i}{3}}$

Tänker vi här att $n$ verkligen bara kan vara vilket heltal som helst? Eftersom $e^{i\theta}$ är periodisk så kommer ju samma värden upprepas flera gånger efter ett antal unika värden. I vårt fall kommer vi få tre unika värden innan upprepning, så det verkar logiskt.

naytte skrev:

Jag förstår inte riktigt vad du menar med detta. Då $a=1>0$ och $b=1/3$ reduceras väl $a^b$ inte till ett entydigt värde?

Lite opedagogiskt av mig men det var tänkt att illustrera hur man använder den "vanliga" reella logaritmen som saknar argument, alltså den entydiga funktion $\ln(a)$ vi kommer ihåg från envariabelanalysen. $1^{1/3}$ är inte entydig i den komplexa kontexten.

 

---

Men om vi tar $1^{1/3}$ som konkret exempel borde vi alltså ha

$\displaystyle \left(1\right)^{1/3}=e^{\frac{1}{3}\left(\ln|1|+i(\mathrm{Arg}(1)+2\pi n)\right)}=e^{\frac{2\pi n i}{3}}$

Tänker vi här att $n$ verkligen bara kan vara vilket heltal som helst? Eftersom $e^{i\theta}$ är periodisk så kommer ju samma värden upprepas flera gånger efter ett antal unika värden. I vårt fall kommer vi få tre unika värden innan upprepning, så det verkar logiskt.

Ja, det blir en mängd med 3 värden. Vi kan till exempel använda $n=0,1,2$ för att generera värdena:

$1^{1/3} = e^{2\pi i n / 3}\Rightarrow 1^{1/3} \in \left\{1,\;-\tfrac{1}{2} + i\tfrac{\sqrt{3}}{2},\;-\tfrac{1}{2} - i\tfrac{\sqrt{3}}{2}\right\}$

Vilka värden på $n$ vi använder spelar i det här sammanhanget ingen roll, så länge vi får fram alla möjliga värden av funktionen. Det finns dock sammanhang där $n$ anger vilket “våningsplan” (eller blad) på Riemannytan vi befinner oss på. Det blir då ett sätt att hålla reda på vilken gren av den flervärda funktionen vi använder.