Komplex analys - är problem av denna typ helt enkelt flervariabla problem?
Halloj!
Jag studerar uppgiften nedan
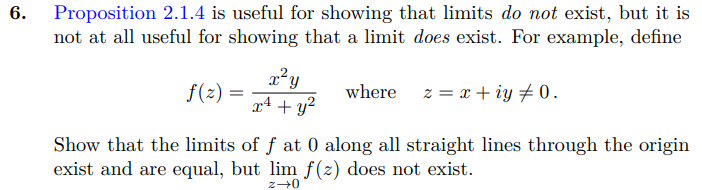
Som vi ser dyker det inte upp något eller någonstans i funktionsuttrycket i HL i funktionsdefinitionen. Innebär detta att problemet egentligen bara är ett flervariabelt gränsvärde i förklädnad, det vill säga vi hade lika gärna kunnat skriva funktionen som
och sedan gränsvärdet som
?
Javisst, om är en helt reell funktion så måste ju existera eller inte existera på precis samma vis, oavsett om vi tänker oss att det är en "komplex funktion" eller en "flervariabel"-funktion eftersom .
Det är först när vi går till derivatan i komplex mening (dvs. som ett gränsvärde av en differenskvot) som begreppen skiljer sig. Ett exempel på det är funktionen som kan få vara . Den är kontinuerlig och deriverbar överallt i , men i det komplexa fallet endast deriverbar i en enda punkt.
Ja, det är riktigt. Man kan säga att det beror på att R^2 och C är isometriska (isomorfa metriska rum) och gränsvärden inte i sig beror av någon annan struktur.
Tillägg: 2 okt 2025 13:31
Missade att frågan redan besvarats
Tack för svar!
@D4NIEL, när du säger att är deriverbar överallt i , vad menar du då? Syftar du på riktningsderivata / partiell derivata?
Ja, jag syftade på det lite hårdare kravet differentierbar för att göra en "rättvis" jämförelse med deriverbar i komplex bemärkelse.
Om en funktions partiella derivator existerar och är kontinuerliga i en omgivning av en punkt, så kan vi dra slutsatsen att funktionen är differentierbar i punkten. Eftersom har kontinuerliga partiella derivator är den som reell funktion betraktad, dvs , differentierbar (deriverbar) i hela . Med det menar vi mer exakt att för varje (i varje punkt) gäller att
Om vi nu jämför med "motsvarande" gränsvärdeskrav för deriverbarhet i det komplexa fallet
ser det ganska likt ut. Men det finns viktiga skillnader som leder till att många reellt differentierbara (deriverbara) funktioner saknar motsvarighet i det komplexa fallet, trots att funktionerna består av "samma reella uttryck", t.ex. och (som bara är deriverbar i en enda punkt).
via i betydelsen



