Komplex Analys - lös reell integral med komplex integral
Halloj!
Jag studerar tentauppgiften nedan
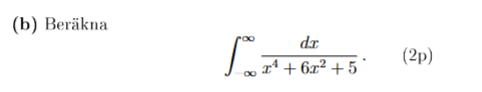
Jag tror att det är meningen att man ska göra om detta till en kurvintegral i . Denna integral är formellt ett gränsvärde:
Sedan kanske man kan tänka att den slutna kurvan vi vill integrera över i kan vara dem som parametriseras de två delkurvorna
Då har vi
Enligt residysatsen vet vi att
där är de punkter i där funktionen inte är holomorf. Hur ska man ta sig vidare härifrån? Jag försöker lära mig genom att lösa uppgifter eftersom jag finner kurslitteraturen väldigt svårsmält så jag ursäkter om detta är "enkelt".
Vi kan börja med att beräkna kurvintegralen och därmed residyerna, vart är funktionen inte holomorf?
Där vi har division med noll. Alltså de punkter som satisfierar . Vi ser snabbt att är en sådan punkt så vi kan faktorisera med polynomdivision:
Men hur ska man faktorisera resten? Gäller det bara att helt enkelt gissa på rötter?
I det här fallet beter sig ungefär som en andragradare, vi har ju inga -termer eller -termer, så vi kan använda kvadratkomplettering/pq-formeln.
Med din gissade rot kan vi också använda satsen som säger att om löser en polynomekvation med reella koefficienter så löser den också
Ah, såklart! Vi gör en substitution . Återkommer.
Jag erhåller rötterna och om jag har tänkt rätt.
Men nu kommer vi till det steget jag har lite svårt att begripa. Hur ska man komma fram till Laurentserieutvecklingen runt dessa punkter? Måste man sitta och manuellt ta fram koefficienterna? Vi behöver ju koefficienten för termen av grad för att beräkna residyerna (denna koefficient kanske till och med ÄR residyn?).
Den koefficienten ÄR residyn, ja. Hur tar du fram koefficienterna i nuläget? Det finns några ganska trevliga sätt att bestämma dem.
Det enda sättet jag är säker på är att kötta med en formel på formelbladet, men det hinner man inte under en tentamen. Jag vet att det finns lite olika regler beroende på vilken typ av pol man diskuterar. Dessa fyra poler skulle väl klassas som enkla poler och om jag minns rätt från föreläsningarna ges residyn i en enkel pol av
Är polerna i den här uppgiften "enkla"?
Dessa poler är enkla, ja. Om är en pol till gäller det även att är en rot till . En pols "ordning/multiplicitet" är densamma som multipliciteten hos roten till . Eftersom alla rötter du har tagit fram till har multiplicitet 1 så gäller det även att de polerna är enkla/har ordning 1.
Om vi istället hade funktionen skulle polen vara av ordning 2, eftersom roten till det polynomet har multiplicitet 2.
Iden bakom formeln du skrev är att i punkten (enkel pol till ) så ges laurentutvecklingen av
För att lösa ut residyn som jag döpt här till , kan vi multiplicera leden med :
Sedan när får vi bara kvar i högerled!
Det enda sättet jag är säker på är att kötta med en formel på formelbladet,
Vi får väl inga formelblad?
Nej, jag menade bara att jag kunde en formel.
Det finns ju fler Residyregler. En säger exempelvis att du kan behålla täljaren, derivera nämnaren och sedan sätta in singulariteterna. Laurent är alltså inte nödvändigt.
Så blir då t.ex. residyn i punkten :
?
Det ser rätt ut!
Noterar. Din kurva omsluter (för tillräckligt stora R)även z=i. Dess residu måste du också ta med för att få det sökta värdet på integralen.
Okej, nu har jag kommit fram till följande:
Om jag nu vil ha , då måste jag ju tillämpa ett gränsvärde då . Då jag gör detta, gäller då följande?
Annars är jag lite osäker på hur man ska beräkna integralen. Frågan är alltså om den komplexa integralen har egenskapen att man kan "flytta in" gränsvärdet?
Det finns en trevlig sats, ML-inequality, för att beräkna dessa. Den säger att om för alla på kurvan , så är
, där
är längden på kurvan .
Jag vet inte om man kan flytta in gränsvärdet.
Längden på är ju , och då har vi ju , så jag är inte riktigt med på hur vi ska använda det.
Däremot kanske man kan triangelolikheta integranden (nämnaren) på något sätt.
Iden är att hitta ett som går snabbare mot än mot . Funktionen i integrandet beter sig ungefär som , så om man finner ett kommer det säkert ha den storleksordningen.
För tillräckligt stora har vi då att är större än integranden. Funkar det? Då beter sig ungefär som medan beter sig som så hela gränsvärdet går mot noll.
Visst! Vi har exempelvis att
och nämnaren är rätt uppenbart större än för stora , vilket ger att integrandet är mindre än
Det finns faktiskt en sats som säger att linjeintegralen av utmed som alltså utgörs av halvcirkeln , , är
om du kan hitta , och så att för alla och gäller
Detta visar man rättframt med ML-olikheten genom valet och längden av kurvan som ni redan påpekat.
En för studenter särskilt användbar variant av satsen med samma bevisidé gäller polynom och ingår förmodligen i er kurs. Den kan lite löst formuleras ungefär så här:
Låt polynomet vara av grad och sakna nollställen utmed x-axeln. Låt vidare polynomet vara av högst grad . Då gäller
På en tenta kan du i de flesta fall hänvisa till någon av satserna, där den senare är mest bekväm. Det finns också en snarlik variant som kallas "Jordans lemma".
Spännande! I den sista satsen du diskuterar som gäller polynom, vad innebär detta?
Res står ju för residy antar jag, men residyerna inom vilket område?
övre halv planet (ö.h.p), dvs summa res för alla poler i övre halvplanet :)
Men leta upp motsvarande sats i er litteratur och använd samma formuleringar, krav och notation som föreläsaren förväntar sig. Det är förmodligen inte tänkt att ni ska behöva föra ett ML-resonemang för varje integral.
Ska bli! Tack för tipset!
Men så för att försöka fullständiga uppgiften:
Vi har för tillräckligt stora att
Vi har då alltså att
för tillräckligt stora . Om vi tillämpar ett gränsvärde ser vi att
Om beloppet av integralen går mot noll måste integralen i sig ge noll då . Så slutligen har vi



