Komplex analys - intuition bakom begreppet homotopi

Halloj!

Jag håller på att läsa på om Cauchys integralsats som lyder

Let $U\subseteq \mathbb{C}$ be an open set, and let $f:U\to \mathbb{C}$ be a holomorphic function. Let $\gamma:[a,b]\to U$ be a smooth closed curve. If $\gamma$ is homotopic to a constant curve, then

$\displaystyle \int_\gamma f\left(z\right)dz=0$

Jag har en del funderingar kring definitionen av homotopi. Den formella definitionen är ganska komplicerad, och helt orimlig att hänvisa till och använda under en tentamen, så jag söker lite intuition bakom begreppet och hur man ska veta om två kurvor är homotopa. Så som jag förstår det är två slutna kurvor homotopa om det är möjligt att kontinuerligt "deformera" den ena till den andra. Är detta en korrekt intuition?

Jag har några frågor utgående från denna definition. Låt säga att vi har integralen nedan

$\displaystyle \int_{|z|=1}\frac{1}{z}dz$

Vad är intuitionen bakom varför denna integral är icke-noll? Den blir ju $2\pi i$ , vilket man ganska enkelt kan räkna fram genom en parametrisering, men varför kan man inte tillämpa Cauchys integralsats här? Varför finns det ingen homotopi mellan enhetscirkeln och t.ex. punkten $z=1/2$ , som självklart ligger i området $\mathbb{C}\setminus \{0\}$ ? Är det för att singulariteten i $z=0$ gör att alla deformationer någonstans skulle behöva löpa genom $z=0$ , vilket hade gjort deformationen icke-kontinuerlig?

Att du inte kan tillämpa Cauchyavsnitt här beror på att f inte är holo på enhetsskivan. Den har en enkelpol i origo..

Ja men $f$ är väl holomorf på $\mathbb{C}\setminus \{0\}$ , vilket är mängden som är aktuell här?

Exakt, vi kan inte kontinuerligt deformera kurvan gamma (enhetscirkeln) till en punkt i C\{0} utan att korsa över z = 0. Tänk att du har en ögla av något elastiskt band och singulariteten z = 0 är en pigg som bandet fastnar på när du försöker dra samman öglan mot någon punkt.

Tillägg: 7 okt 2025 15:05

Det är alltså inte att deformationen inte kan vara kontinuerlig, utan snarare att 0 inte ingår i mängden som kurvorna befinner sig i.

Okej, tack! Så om vi hade valt en annan kurva $\gamma$ , t.ex. en avskuren linje från $z=1$ till $z=1+2i$ , visst hade vi då kunnat tillämpa Couchys integralsats på

$\displaystyle \int_\gamma \frac{1}{z}dz$

för vi kan definitivt hitta en punkt på denna linje vi kan deformera hela linjen kontinuerligt till, t.ex. $z=1+i$ ?

Cauchy sats gäller för slutna kurvor. Sträckan mellan z=1 och z=1+2i är ingen sluten kurva, men om du kompletterar den till en sluten kurva så att origo ligger utanför det du innesluter så ger Cauchy att integralen blir 0.

Ah, såklart! Missade "closed" i definitionen. Låt säga att vi tar vilken cirkel som helst som inte innehåller origo istället. Skulle det gå då?

Hmm, strunt samma angående detta inlägg har jag kommit fram till.

Jag tyckte att inlägget var lärorikt. Jag följde varje uppdatering med intresse.

Det jag tror jag försökte säga var bara att det finns några snarlika men olika sätt att definiera homotopier på. För det mesta brukar en förutsättning vara att de har samma ändpunkter. Detta kallas ibland för "path homotopy". En kurva från 1 till 1+2i skulle således aldrig kunna vara homotop med en konstant kurva (en kurva vars bild endast är en punkt) i denna bemärkelse.

Om vi däremot begränsar oss till slutna kurvor, så behöver vi inte ställa kravet på att baspunkten (ändpunkten/startpunkten) för kurvorna ska vara samma under hela den kontinuerliga deformationen, utan den punkten kan tillåtas att flyttas. Ibland brukar man ändå kräva att baspunkten är densamma. Det finns slutna kurvor som är "fritt" homotopa (vi tillåter baspunkten att ändras under deformationen) men inte homotopa om baspunkten måste vara fixerad.

Jag försökte illustrera skillnaden med en bild:

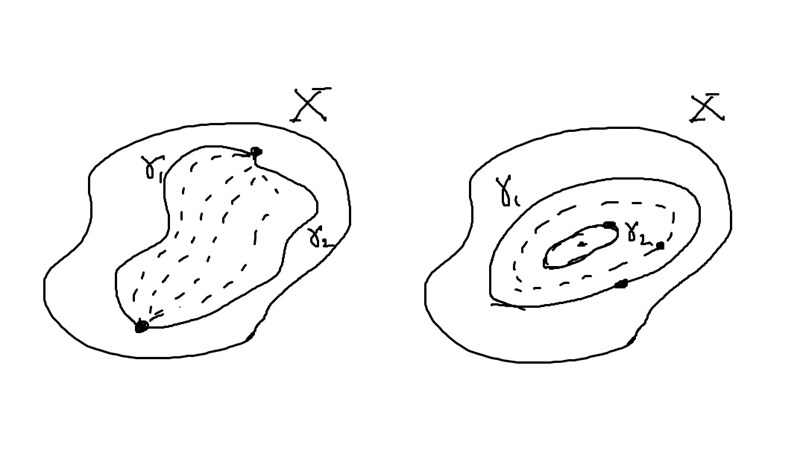
Till vänster är $\gamma_1$ och $\gamma_2$ homotopa i den första bemärkelsen och till höger är de nu slutna kurvorna $\gamma_1$ och $\gamma_2$ homotopa i den andra bemärkelsen. För båda dessa besläktade begrepp gäller att om $f:X\to\mathbb{C}$ är någon holomorf funktion på en öppen, sammanhängande mängd $X\subset\mathbb{C}$ så är

$\int_{\gamma_1}f(z)dz = \int_{\gamma_2}f(z)dz$ (En version av Cauchys integralsats).

Om $\gamma$ är en konstant kurva så är $\gamma'(t)=0$ , vilket innebär att $\int_\gamma f(z) dz =0$ . Resultatet ovan visar då att integralen av $f$ längs varje kurva homotop med en konstant kurva måste bli lika med noll.

Om vi släpper kravet på att ändpunkterna ska vara samma i den första definitionen så kan varje öppen kurva deformeras till en punkt. Om $\gamma:[0,1]\to X$ är en kurva i något rum $X$ (tag $X=\mathbb{C}$ om du vill) så kan vi definiera

$H(t,x) := \gamma((1-t)x),\quad t,x\in [0,1]$ .

Då återfår vi kurvan $\gamma$ om vi fixerar $t=0$ som $H(0,x)$ , och om $t=1$ så är $H(1,x)=\gamma(0)$ . Låter vi $t$ gå från 0 till 1 så har det effekten att $\gamma$ "dras ihop" mot sin startpunkt $\gamma(0)$ . För $t=0.5$ till exempel så är $H(t,x)$ den kurva som går mellan $\gamma(0)$ och $\gamma(0.5)$ .

Svara

Visa senaste svar