Komplexa tal. Vilka värden på a?

Tekniskt sett är reella tal komplexa också, så även om det vore möjligt att $\mathrm{Im}(ai)=0$ så hade $ai$ fortfarande varit komplext.

Men hur som helst är det väl inte så krångligt att motivera att han har rätt? Det enda sättet för $ai$ att bli reellt är om $a$ har nollskild imaginärdel, vilket vi vet inte är sant.

Om a är ett reellt tal så saknar det imaginärdel. a*i kommer då per definition vara rent imaginärt, så talet blir komplext.

Men imaginärdelen är sin(lna) som ju blir 0 då a = 1?

Varför undersöker du $a^i$ och inte $ai$?

Skrev du fel i frågan här eller fel till ChatGPT?

Självaste frågan:

Kanske blev det ett missförstånd? Skrev jag fel någonstans?

Facit (som jag inte förstår):

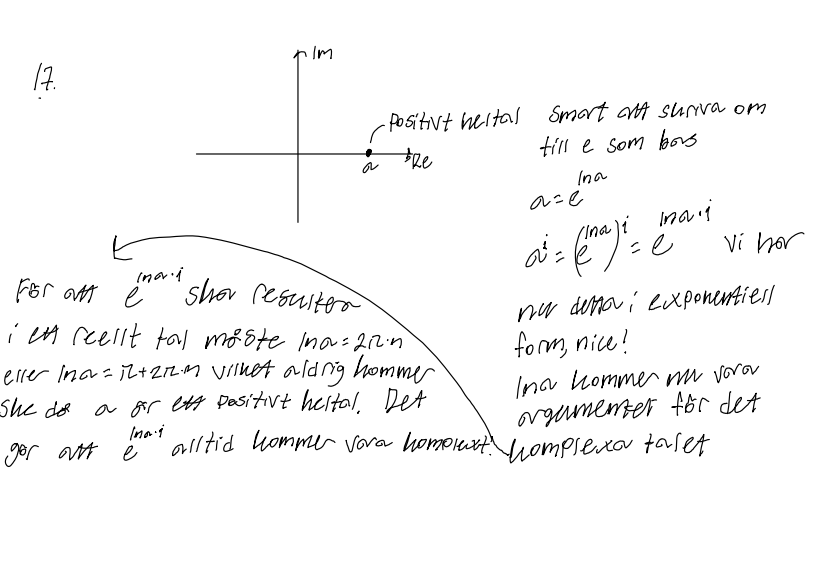
Om n=0 blir ln a = 0 och a=1. 

Ja, du råkade skriva $ai$ istället för $a^i$, men ingen fara, då vet vi.

Men du har rätt. Om vi stoppar in $a=1$ får vi ett tal som har imaginärdel noll.

Men med detta sagt är frågan felformulerad. Även om imaginärdelen blir noll har Joakim rätt eftersom alla reella tal är komplexa.

Har 2 frågor också:

1. Kan man göra detta genom att ansätta z på polärform eller rektangulär form också?
2. Om nej, hur vet jag att det enbart går att lösa med potensform?

(1) Vet inte hur du skulle ansätta $z$ på polär- eller rektangulär form. Det kanske går men frågan är om det är praktiskt. Att höja i basen $e$ är ett "standardknep" som är väldigt användbart.

(2) Svaret på den frågan är väl detsamma som svaret på frågan "hur vet jag att man ska lösa $x^2-1=0$ genom att lägga till ett på båda sidor och ta plus-minus-roten-ur?". Man lär sig genom att göra helt enkelt och känna igen när vissa angreppssätt lämpar sig.