Komplexa tal, z^4
Hej, jag har kommit fram till att den första rena imaginära lösningens konjugat också är en lösning.
försökte göra polynomdivisiion, men det blev krångligt. Dividerade då med båda lösningarna samtidigt (z-ai)(z-bi)
hur ska man göra? Tacksam för hjälp

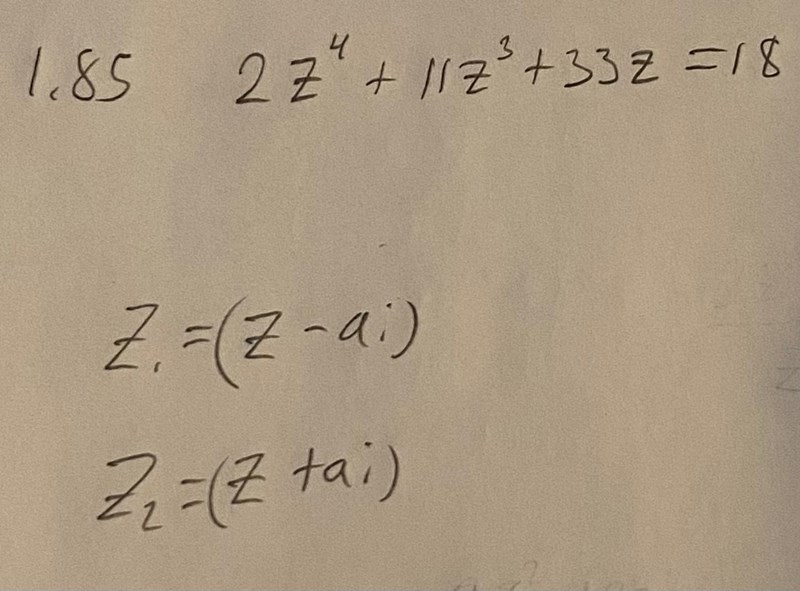
Hej.
Eftersom koefficienterna är reella tal så dyker de komplexa lösningarna upp i komplexkonjugerade par.
Det betyder att om är en lösning så är även en lösning.
Bestäm nu värdet på och utför sedan polynomdivision med , dvs med , dvs med .
Låter bra, men hur bestämmer jag a?
Ja, det blir ju en fjärdegradsekvation i a, vilket inte är helt enkelt att lösa, speciellt eftersom a inte blir ett heltal.
Du kan pröva att hitta eventuella reella rötter istället med hjälp av satsen om rationella rötter.
Jag skulle sätta in z = i*a.
Real- respektive imaginärdelar ska vara lika på båda sidor likhetstecknet.
Dr. G skrev:Jag skulle sätta in z = i*a.
Real- respektive imaginärdelar ska vara lika på båda sidor likhetstecknet.
@Yngve, testar Dr.G:s metod först. Tack
@Dr.g - Jag vet att om z=ai blir uttrycket 0. Om jag sätter z=ai, då får jag ett ekv syst som ger: x=0, y=a (z=x+yi). Kommer inte längre då.
hur menade du?
Dr. G skrev:Jag skulle sätta in z = i*a.
Real- respektive imaginärdelar ska vara lika på båda sidor likhetstecknet.
Just det, vi har ju både jämna och udda z-exponenter, vilket gör att vi har både real- och imaginärdelar i ekvationen.
Vi vet att det finns en rot
(och då är även konjugatet en rot p.g.a reella koefficienter.)
Insättning ger
Dela upp VL i real- och imaginärdelar. Lös ekvationssystemet.
Dr. G skrev:Vi vet att det finns en rot
(och då är även konjugatet en rot p.g.a reella koefficienter.)
Insättning ger
Dela upp VL i real- och imaginärdelar. Lös ekvationssystemet.
Smart, din kunskap om komplexa tal är imponerande. 👍🏻
Fick rätt nu.
z=isqrt(3)
z=-isqrt(3)
z=1/2
z=-6




