Kontinuitet

Menar du de tre punkterna om kontinitet? I så fall, varför beskär du inte bilden så att vi slipper gissa?

Ja och ja

• Punkt 1 säger att om det går att rita en funktions graf utan att lyfta pennan så är funktionen kontinuerlig. Exempel: f(x) = x²
• Punkt 2 säger att om det inte går att rita en funktions graf utan att lyfta pennan så är funktionen diskontinuerlig: Exempel $f(x)=x^2$ då $x\neq1$, $f(x)=0$ då $x=1$
• Punkt 3 säger att om en funktions definitionsmängd endast består av vissa punkter så är funktionen diskret. Exempel: f(x) = antal mynt av varje valör i en myntsamling.

EDIT - ändrade riktning på implikationerna och bytte ut exemplet I punkt 2.

Yngve jag hänger inte riktigt med dig på den tredje punkten

Tillägg: 10 jul 2024 09:12

Eller vad menas med punktvis definerade, finns något exepel på en funktion som jag vet när jag skriver in y= nånting ?

Säg att du har en myntsamling.

I den har du mynt av olika valörer, t.ex. 1, 2, 5 och 10 kronor.

Du kan nu ange en funktion som beskriver hur många mynt du har av varje sort.

Definitionsmängden består endast av talen 1, 2, 5 och 10.

Du kan ha en enkrona eller två enkronor, men du kan inte ha 1,5 eller 2,73 enkronor.

Arup skrev:

---

Tillägg: 10 jul 2024 09:12

Eller vad menas med punktvis definerade, finns något exepel på en funktion som jag vet när jag skriver in y= nånting ?

Ett bra exempel på en sådan diskret funktion hittar du här.

Tack, är det hör ett exempel på en diskret funktion (det blåa) ?

Nej, både f(x) och g(x) är icke-diskreta eftersom deras definitionsmängder inte endast består av vissa punkter.

Jag formulerade om mitt svar #4.

Problemet med bilderna i inlägg #9 är att den vänstra är kontinuerlig trots att den inte kan ritas med ett enda streck - det beror på att den punkt där den "hoppar" inte ingår i definitionsmängden. Med detta synsätt (som jag tror härskar på universiteten, men inte på gymnasiet) är även f(x) = 1/x en kontiunuerlig funktion, eftersom x = 0 inte ingår i definitionsmängden.

Smaragdalena skrev:

[...[ är även f(x) = 1/x en kontiunuerlig funktion, eftersom x = 0 inte ingår i definitionsmängden.

Det stämmer. Jag har ändrat exemplet vid punkt 2 i svar #4.

Yngve jag tolkade #4 som om det vore en ordinarie linjär funktion

Arup skrev:

Yngve jag tolkade #4 som om det vore en ordinarie linjär funktion

I svar #4 försökte jag förklara de tre begreppen. Vad var det du tolkade som en linjär funktion?

punkt 3

En linjär funktion kan generellt beskrivas som f(x) = kx+m, där k och m är konstanter.

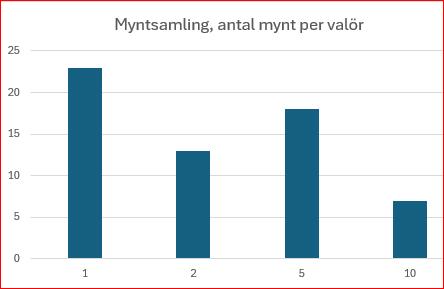
I fallet med myntsmlingen (punkt 3) kan vi t.ex. ha

• f(x) = 23 då x = 1, dvs vi har 23 st enkronor.
• f(x) = 13 då x = 2, dvs vi har 13 st tvåkronor.
• f(x) = 18 då x = 5, dvs vi har 18 st femkronor.
• f(x) = 7 då x = 10, dvs vi har 7 st tiokronor.

Detta går inte att beskriva med hjälp av f(x) = kx+m.

Se bild, f(x) är inte en linjär funktion.

Här har jag ritat upp en kontinuerlig och en diskret funktion.

Med detta synsätt (som jag tror härskar på universiteten, men inte på gymnasiet)

Detta är väl egentligen det enda synsättet som finns? I exemplet till vänster kan man säga att definitionsmängden är diskontinuerlig men att funktionen är kontinuerlig på hela sin definitionsmängd.

@Arup, det som följer nedan är överkurs:

Definitionen (och såvitt jag vet den enda?) för kontinuitet i metriska rum är ju:

Låt $\displaystyle f:D_f\to\mathbb{R}$. $f$ är kontinuerlig runt en punkt $x=c$ om och endast om det för alla $\epsilon > 0$, finns ett $\delta > 0$, sådana att $\displaystyle |f\left(x\right)-f\left(c\right)|<\epsilon$, när $\displaystyle |x-c|<\delta$ och $x,c\in D_f$.

och här är ju en förutsättning för kontinuitet i en punkt att $c$ ingår i definitionsmängden.