Koordinater i enhetscirkeln
Detta gäller uppgift 6 a) i bilden nedan. I a), gör jag rätt om jag rent bildligt kan resonera mig fram till att Q's koordinater med stor sannolikhet är (-b, -a) eftersom det ser ut att vara så. Eller finns det ett något sätt att bevisa det?
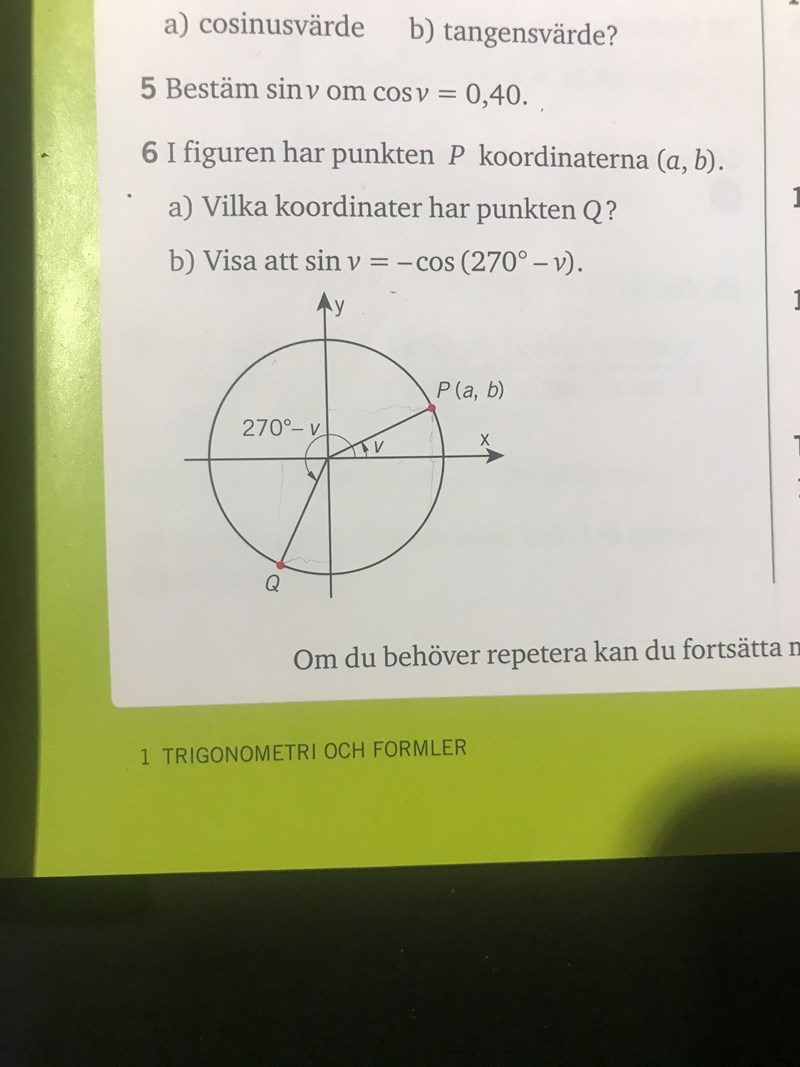
"Ser ut så" är knappast tillräckligt. Naturligtvis kan man bevisa det, annars skulle du inte förväntas kunna svara.
"Ser ut så" är helt ok för att komma på vad det är man ska bevisa, inget fel med det, men sen ska man bevisa det.
Det kanske kan underlätta om du ser på 270-v som en differens av två vinklar istället för en "egen" vinkel. Kan du göra något i den tankebanan? Hur hanter man summor och differenser av vinklar i den här typen av trigonometri?
Jag skulle nog undvika trigonometriska formler och istället använda att de bäda trianglarna OMP och ONQ är kongruenta.
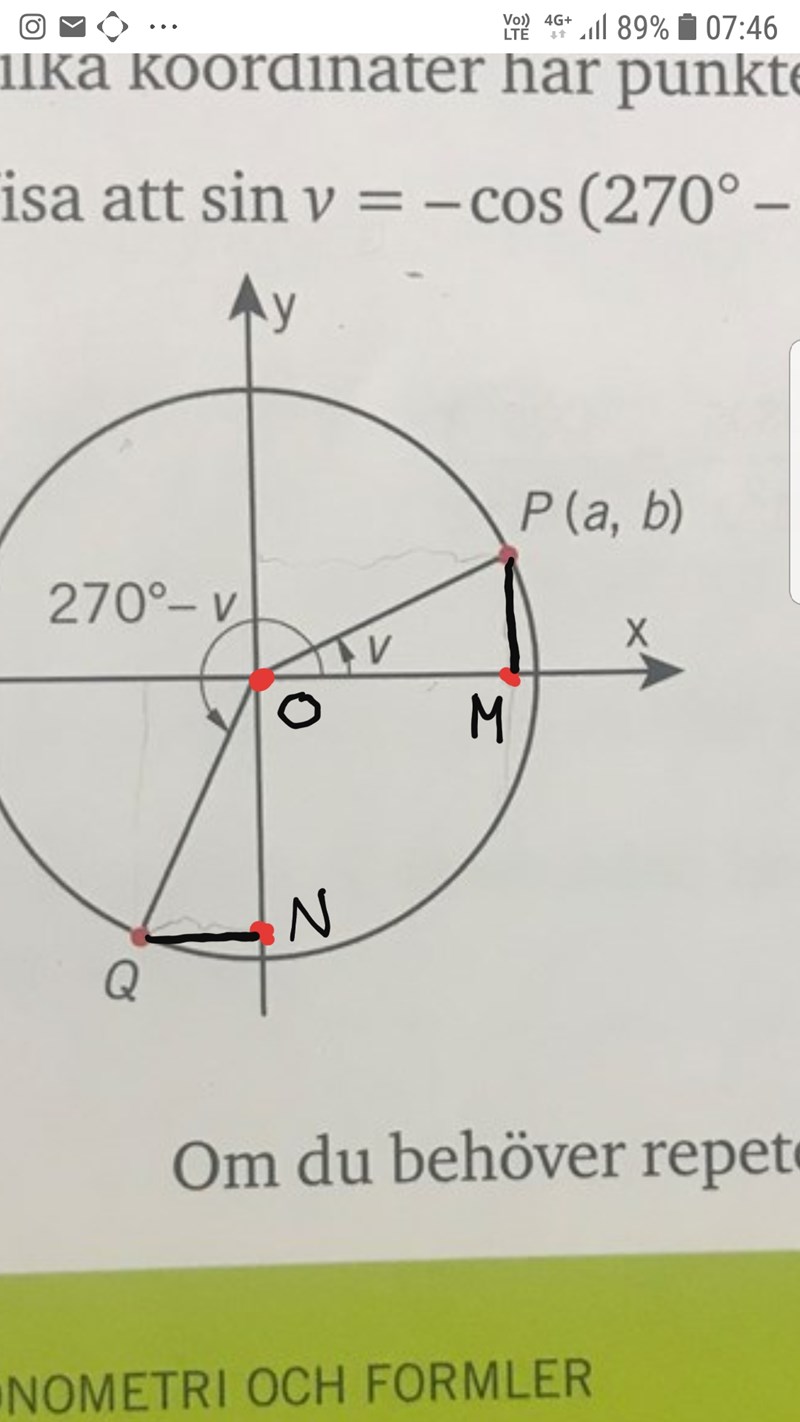
Vi ser av figuren att vinkeln mellan Y-axeln och linjen till punkten Q i tredje kvadranten måste vara - v
Det medför som Yngve konstaterat att vi har två likformiga trianglar och att avståndet i x-led i tredje kvadranten är lika stort som avståndet i y-led i första kvadranten, men med negativt förtecken.
Om vi ritar in de uppgifterna i cirkeln så ser det ut så här:
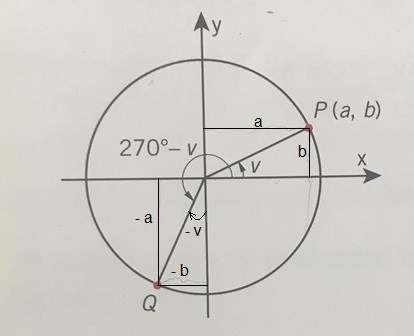
Därav kan vi dra slutsatsen att punkten Q kan skrivas
Tackar för svaren!
Yngve skrev:Jag skulle nog undvika trigonometriska formler och istället använda att de bäda trianglarna OMP och ONQ är kongruenta.
Med det blir ju så fint och i ett led med trig-formler :)
-cos(270-v) = -(cos 270 * cos v + sin 270 * sin v) =-(0*cos v - 1*sin v) = -(-sin v) = sin v
cjan1122 skrev:
Med det blir ju så fint och i ett led med trig-formler :)
-cos(270-v) = -(cos 270 * cos v + sin 270 * sin v) =-(0*cos v - 1*sin v) = -(-sin v) = sin v
Orsaken till att jag skulle undvika dessa är att jag misstänker att syftet med uppgiften var just att visa att formeln stämmer.
Yngve skrev:cjan1122 skrev:Med det blir ju så fint och i ett led med trig-formler :)
-cos(270-v) = -(cos 270 * cos v + sin 270 * sin v) =-(0*cos v - 1*sin v) = -(-sin v) = sin v
Orsaken till att jag skulle undvika dessa är att jag misstänker att syftet med uppgiften var just att visa att formeln stämmer.
Dessutom är det du svarat cjan1122, svaret på b) och inte på a) som eleven frågade efter, men det var bra ändå att du visade hur det skulle gå till :-)
Edit: Mitt svar är alltså till cjan1122




