Kortaste vertikala avståndet d
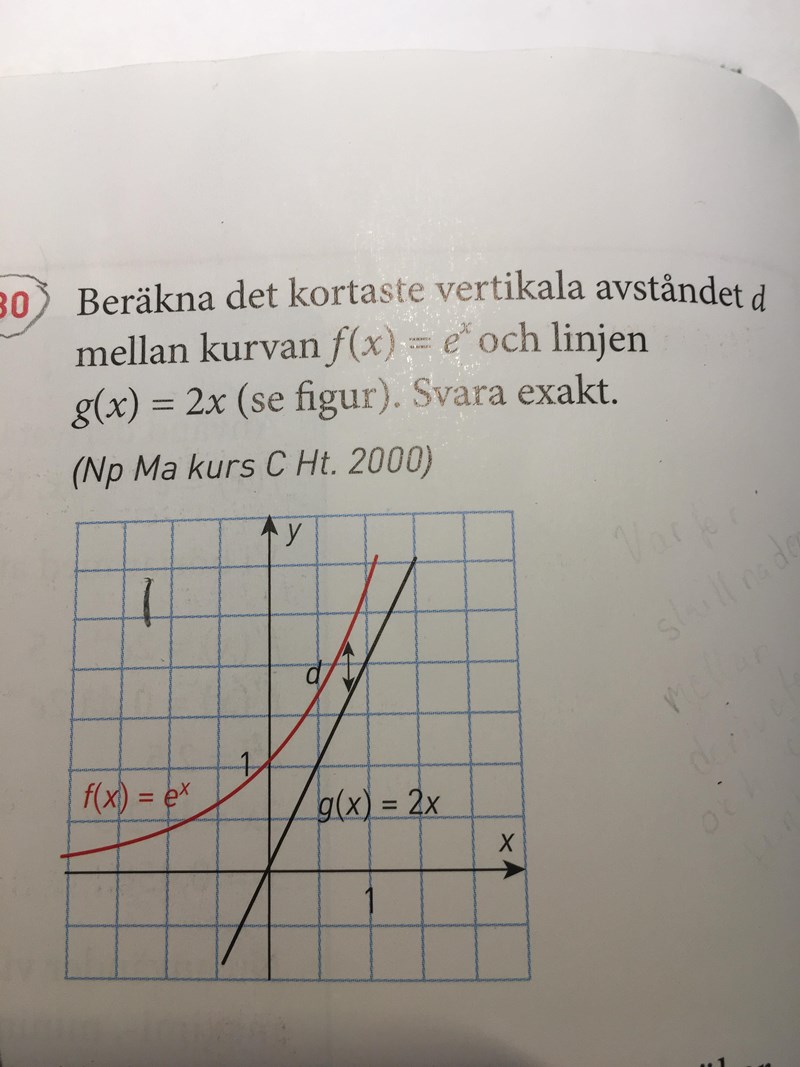 Avståndet mellan de ska vara så kort som möjligt alltså 0. Avståndet kan beskrivas som skillnaden mellan funktionernas derivator:
Avståndet mellan de ska vara så kort som möjligt alltså 0. Avståndet kan beskrivas som skillnaden mellan funktionernas derivator:
d=0= e^x-2
Men hur ska jag lösa detta för jag får det bara till X=ln(2). ( som tyvärr är fel ;( )
Visa spoiler
Facit:

Nej avståndet är inte skillnaden mellan derivatorna.
Det vertikala avståndet vid en viss x-koordinat är skillnaden mellan funktionsvärdena vid den x-koordinaten, dvs (egentligen ).
Det är detta avstånd som du ska minimera, men det är inte säkert att avståndet är lika med 0 någonstans.
Istället ska du använda derivata för att hitta det minsta värdet som detta avstånd kan anta.
Yngve skrev:Nej avståndet är inte skillnaden mellan derivatorna.
Det vertikala avståndet vid en viss x-koordinat är skillnaden mellan funktionsvärdena vid den x-koordinaten, dvs (egentligen ).
Det är detta avstånd som du ska minimera, men det är inte säkert att avståndet är lika med 0 någonstans.
Istället ska du använda derivata för att hitta det minsta värdet som detta avstånd kan anta.
Det gjorde jag först men sedan sa facit att man skulle räkna med derivatorna ?
Vänta jag kom på det, det riktiga avståndet är som det står f(X) - g(X) men sedan räknar man på skillnaden mellan derivatorna för att få X-värdet ?
så att X= ln(2) var rätt man måste bara sätta in den i skillnaden
Du ska minimera uttrycket .
För att hitta eventuella min/maxpunkter så kan du derivera uttrycket och sätta derivatan lika med 0.
Yngve skrev:Du ska minimera uttrycket .
För att hitta eventuella min/maxpunkter så kan du derivera uttrycket och sätta derivatan lika med 0.
Ja precis och minimipunkten mellan de båda funktionerna är det minsta avståndet och det X-värdet som söks!
Ja. Du bör även visa att det x-värde du hittade verkligen ger en min- och inte en maxpunkt.
Yngve skrev:Ja. Du bör även visa att det x-värde du hittade verkligen ger en min- och inte en maxpunkt.
Då kan jag bara sätta in ett lite högre X-värde i funktionen och ett lite mindre X-värde t.ex. ln(1) och ln(3)
om båda ger högre y-värde än ln(2) vet jag att det är en minimi-punkt .
Ja det stämmer.
Det går även att visa med hjälp av andraderivatans tecken, men det lär du dig nog senare.
Yngve skrev:Ja det stämmer.
Det går även att visa med hjälp av andraderivatans tecken, men det lär du dig nog senare.
Teckenstudium ?
linnea.matte skrev:Yngve skrev:Ja det stämmer.
Det går även att visa med hjälp av andraderivatans tecken, men det lär du dig nog senare.
Teckenstudium ?
Funkar också. Som så ofta finns det flera olika sätt att komma fram till samma svar.



