Lagrange

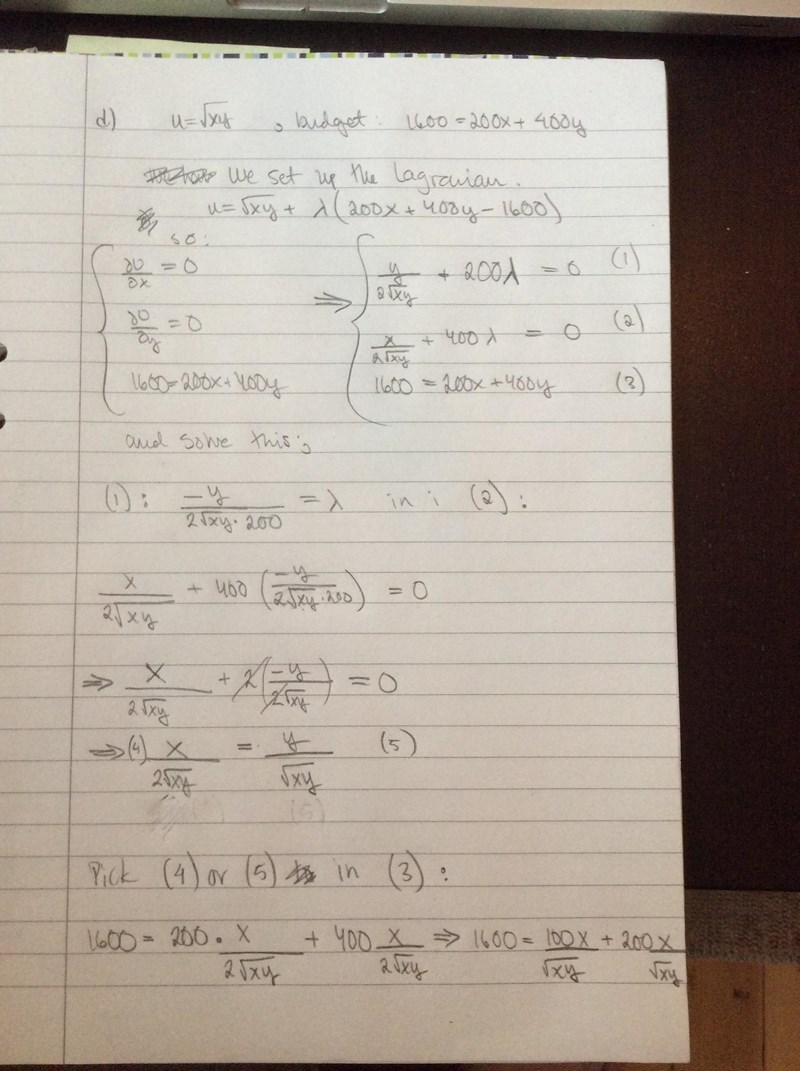
Vad är det jag snurrar till det? för det känns inte alls rätt det här....
Du har ju inte fullföljt räkningarna så det är svårt att säga var det leder.
Men jag kan anmärka på att ditt ekvationssystem hade blivit lite enklare att hantera om du istället för att hålla på med
hade skrivit dessa kvoter som
Dvs undvika att ha x eller y i både täljare och nämnare i kvoterna. Om du undviker detta blir både manipulationerna enklare att göra och det blir tydligare var de sakerna du ska lösa ut sitter i uttrycken.
Du har skrivit att utan att förenkla det till . Detta skulle ge dig mycket enklare siffror i fortsättningen.
Uppgiften är att finna så att nyttofunktionen blir så stor som möjligt, under förutsättning att uppfyller bivillkoret .
Lagrangefunktionen är där .
Dess gradient är vektorfältet
och den sökta optimala konsumtionen finner bland bland vektorfältets nollställen ;
samtidigt som
vilket medför att och insatt i bivillkoret får man vilket ger den kritiska punkten till Lagrangefunktionen.



