Lån, amortering, annuitet...

Hej, håller just nu på med geometriska summor i matematik och många uppgifter handlar om lån amorteringar och annuitet. Jag vet inte hur allt hänger ihop och hur geometriska summor kommer in i bilden. Är det någon som skulle kunna förklara?
Tack på förhand!
Det är lite för komplicerat för att presenteras i ett vanligt inlägg.
Kolla först vad det står om saken i din kursbok.
Begrepp: lån (skuld), löptid, amortering, ränta, annuitet
Men här lite om bakgrunden:
Hur skiljer sig ett annuitetslån från ett vanligt lån och vad är poängen med det?
Amortering betyder återbetalning.
Ett "vanligt" lån har "rak amortering". Då betalar man varje år tillbaka samma andel av den ursprungliga skulden (alltså samma belopp varje år, konstant årlig amortering). Till det kommer ränta på den kvarstående skulden (som minskar med varje amortering). Detta gör att de årliga betalningarna [amortering + ränta] kan bli mycket olika stora över lånets löptid.
De blir HÖGA i början och avtar sedan efter hand som man amorterar.
De första årens betalningar kan rentav bli mer än man klarar av.
Om man i stället låter amorteringarna vara små i början och stora mot slutet, så får vi en jämnare betalningföljd. Summan av dem ska dock fortfarande vara lika med den ursprungliga skulden – vi ska betala tillbaka det vi har lånat, varken mer eller mindre.
I ett annuitetslån har vi anpassat amorteringsföljden så att summan [amortering + ränta] blir lika stor varje år. Jämnare betalningsföljd än så finns inte.
Det är då som [amortering + ränta] kallas annuitet.
21.7% skulle jag tro.
Min fråga lite tydligare formulerad:

Och varför just x utgör annuiteten?
Trinity2 skrev:21.7% skulle jag tro.
Det stämmer.
Din formel anger sambandet mellan
lånebelopp L
löptid i år n
årsräntesats r (dvs 100·r%)
annuitet a (det bär mig emot att beteckna annuiteten med något annat än a )
Det ekonomiska sambandet är att
lånebeloppet, L ,
ska var lika med
summa nuvärde av de framtida annuiteterna,
som på matematiska kan skrivas:
Utveckla summan och kolla!
Just det. Du skriver framtida annuiteterna, men har inte annuiteterna samma värde hela tiden? Dvs. de är konstanta? Hur får du fram uttrycket där exponenten är -k?
Detta:
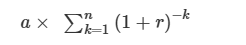
Visst, de är konstanta, men de betalas vid framtida tidpunkter,
så nuvärdet av varje annuitet avtar efter han som tiden går.
Ok, skulle du säga att formeln som jag visar i inlägg 4 alltid kan användas för att beräkna en annuitet? Jag förstår nämligen fortfarande inte hur allt hänger ihop med geometrisk summa.
Högerledet i sambandet är produkten av en konstant och en geometrisk summa
Ok. Men denna metod fungerar alltid då en annuitet ska beräknas?
Sambandet i #8 gäller generellt,
dvs att lånebeloppet är lika med summa nuvärde av annuiteterna
under lånets löptid.
Ok. Sambandet är detsamma i inlägg 4?
Vet inte. Varifrån kommer den?
Beräkna summan i #8 och se vad du får.
Var försiktig! Observera att L som nämns som "lånebelopp" i inlägg 4 inte är samma L som Arktos definierar i inlägg 6.
Arktos räknar med nuvärden, L i inlägg 4 är däremot det framtida värdet av lånebeloppet.
Ta ett enkelt exempel (med Arktos symboler):
L = 700
n = 3
r = 100% -> ff = 2 // ff från inlägg 4
a = ?
Hur mycket är du skyldig banken i slutet av varje år:
år 0: L
år 1: L*ff - a
år 2: (L*ff - a)*ff - a
år 3: ((L*ff -a)*ff -a)*ff -a = 0 // Du har betalat tillbaka allt
Den sista raden kan skrivas om till:
L*ff3 = a * (ff2 + ff + 1) // här är den geometriska summan
Observera att det är L*ff3 (=5600kr) som inlägg 4 kallar L, lånebelopp (Lite missvisande, tycker jag. Jag skulle kalla 700 kr som jag får i början för "lånebelopp".)
Med våra värden blir a= 800 kr
Skulden i slutet av:
år 0: 700kr
år 1: 2*700kr - 800kr = 600kr
år 2: 2*600kr - 800kr = 400kr
år 3: 2*400kr - 800kr = 0
OBS Om du delar både VL och HL med ff3 (dvs beräknar nuvärdet) får du Arktos ekvation.
Anonym_15 skrev:Hej, håller just nu på med geometriska summor i matematik och många uppgifter handlar om lån amorteringar och annuitet. Jag vet inte hur allt hänger ihop och hur geometriska summor kommer in i bilden. Är det någon som skulle kunna förklara?
Så detta är ett avsnitt om geom. summor och de tillämpar detta på annuitet först i övningarna och inte i några exempel? Annuitet m.m. är inte helt självklart om man inte utsatts för bankvärlden, vilken man knappast har som tonåring. Det kräver lite studier i hur banker tänker och hur lån fungerar. Märkligt att inte det finns en mängd exempel på detta i läroboken innan man skall öva på det.
Tack för alla svar. Ja, en hel del uppgifter om lån, annuitet och ränta i avsnittet om geometriska summor. Har precis nu börjat förstå lite, men långt ifrån allt.
Anonym_15 skrev:Tack för alla svar. Ja, en hel del uppgifter om lån, annuitet och ränta i avsnittet om geometriska summor. Har precis nu börjat förstå lite, men långt ifrån allt.
Skulle du kunna visa bilder på teorin för annuitet i din bok? Det skulle vara intressant och se vad de skriver och det presenteras.
Det finns ej i våran bok. Ingenting om varken lån eller annuitet. Men enligt vår lärare ska vi kunna detta eftersom det hör ihop med geometrisk summa.
Anonym_15 skrev:Det finns ej i våran bok. Ingenting om varken lån eller annuitet. Men enligt vår lärare ska vi kunna detta eftersom det hör ihop med geometrisk summa.
Så denne menar att ni skall lära er geom. summa och sedan fundera ut annuitet själva? Märkligt. Men, skolan kanske ändras och med internettillgång skall man göra sin egen lärobok i Ma5? Det är som att säga "Kan du klockan, då kan du moduloräkning, sätt igång nu".
(Ge läraren 'von Neumanns fluga' och se hur han löser det... Det finns en omständig metod och en enkel. Man brukar skämtsamt säga att det är ett test om man är fysiker eller matematiker...)
Som ett exempel på geometrisk serie kan man se det så här (med reservation för räknefel):
Kalla skulden B, räntesatsen p, annuiteten A, och de årliga avbetalningarna ai.
Då får man för de första åren:
a1 +p(B) =A
a2 + p(B -a1)=A
a3+ p (B- a1 -a2)=A
och a3 = a2p
Hade vi tittat på fallen an+1 och an med snyggt utskrivna delsummor (prova gärna) hade
vi fått
an+1 = an p
och
an+1 = a1 (1+p)n
och därmed den geometriska serien (1+p)n
Sen kan man snickra vidare för koppla ihop till annuiteten.
hansa skrev:Som ett exempel på geometrisk serie kan man se det så här (med reservation för räknefel):
Kalla skulden B, räntesatsen p, annuiteten A, och de årliga avbetalningarna ai.
Då får man för de första åren:
a1 +p(B) =A
a2 + p(B -a1)=A
a3+ p (B- a1 -a2)=A
och a3 = a2p
Hade vi tittat på fallen an+1 och an med snyggt utskrivna delsummor (prova gärna) hade
vi fått
an+1 = an p
och
an+1 = a1 (1+p)n
och därmed den geometriska serien (1+p)n
Sen kan man snickra vidare för koppla ihop till annuiteten.
Det finns lite olika sätt att närma sig detta har jag märkt.
-- Subtraktion av annuiterna A från skulden och förräntning. Detta kan efter ca. 3 steg förenklas med geometrisk summa och man kan ana den slutna formeln (vilken strikt behöver ett induktionsbevis vilket även ingår i Ma5, tror jag)
-- Det slutliga sammanlagda värdet av samtliga annuiteter som då skall motsvara den förräntade skulden. Detta brukar förekomma i vissa böcker.
Sedan finns de säkert andra ingångar.
Jag vet inte vilken som är bäst. Annuitet är inte ett främmande begrepp "IRL" så man undrar varför detta inte är upptaget i Ma5-teorin utan "lämnas till läsaren".
Trinity2 skrev:Anonym_15 skrev:Det finns ej i våran bok. Ingenting om varken lån eller annuitet. Men enligt vår lärare ska vi kunna detta eftersom det hör ihop med geometrisk summa.
Så denne menar att ni skall lära er geom. summa och sedan fundera ut annuitet själva? Märkligt. Men, skolan kanske ändras och med internettillgång skall man göra sin egen lärobok i Ma5? Det är som att säga "Kan du klockan, då kan du moduloräkning, sätt igång nu".
(Ge läraren 'von Neumanns fluga' och se hur han löser det... Det finns en omständig metod och en enkel. Man brukar skämtsamt säga att det är ett test om man är fysiker eller matematiker...)
"Kan du klockan, då kan du moduloräkning, sätt igång nu". På pricken!
Uppgifter om annuitetslån och annuiteter återkommer år efter år. I mitt första inlägg (#2) svarade jag att det är lite för komplicerat att gå igenom hela bakgrunden i ett vanligt inlägg. Man behöver vara bekant med en hel hop grundläggande ekonomiska begrepp, termer och samband för att få ihop det. Egentligen är detta en ekonomiuppgift och ingen matteuppgift, men man översätter den till matematiska för att kunna lösa den. Precis som man gör med fysikuppgifter.
För flera år sedan gjorde jag ett försök att gå hela vägen, från en "enkel" uppgift om ett annuitetslån och fram till härledning av en formel för beräkning av en godtycklig annuitet. Den enda matematik man behöver är summan av en geometrisk talföljd. Resten är ekonomi och det beskriver jag efter hand som det behövs.
Här kommer det i repris.
Häng gärna med ända fram till formeln + räkneexempel
Fråga om något är oklart.
https://www.pluggakuten.se/trad/problemlosning-procent-11/
Länken leder till sista delen av tråden. Skrolla tillbaka till början.
Plötsligt försvann hela mitt inlägg!
Förargligt. Det har hänt förut..
Återkommer i morgon
Arktos skrev:Plötsligt försvann hela mitt inlägg!
Förargligt. Det har hänt förut..
Återkommer i morgon
Anmärkningsvärt att det inte finns någon bra skrift i ämnet. Har inte ekonomins högborg, Handels i Stockholm, något bra kompendium i grundläggande ekonomisk matematik?
I.a.f. får väl vi skriva ett :)
"Jag har ingen bra förklaring till det just nu, men det funkar så".
– Matematiklärare(?) i svensk skola, A.D. 2020
https://www.youtube.com/watch?v=m6cYYf3vAiU
Jag gillar att han fokuserar på vad som kommer upp på ett NP, istället för att lära ut en kunskap/metodik 'för livet'...
Se även lösningsförslaget i denna tråd:
https://www.pluggakuten.se/trad/geometrisk-summa-och-annuitet-1/
Videon ovan verkar vara en hastig repetition för de egna eleverna inför provet.
En grundbult är att betrakta (1+r)k som växelkursen mellan
[1 kr vi får om 0 år] dvs NU, och [1 kr vi får om k år]
Värdet av belopp som utfaller vid olika tidpunkter kan därför inte jämföras direkt.
Vi måste först växla dem till belopp som utfaller vid samma tidpunkt:
[1 kr nu] är lika mycket värd som [(1+r)k kr om k år]
[1 kr om k år] är lika mycket värd som [(1+r)-k kr nu]
Man säger då att {nuvärdet av [1 kr om k år]} = (1+r)-k kr
Kanske det förklarar sambandet i #6 ,
det samband vi använder för att beräkna annuiteter ?
Om allt är rätt räknat, ska
den ursprungliga skulden
vara lika med
det sammanlagda nuvärdet av alla annuiteterna

