Linjär algebra 2, delrum

Hej,

I vår bok står följande exempel på vad som är ett delrum till ett vektorrum.

(1) $A l l a s y m m e t r i s k a n \times n - m a t r i s e r ä r e t t d e l r u m t i l l M_{n m}$

(2) $l^{2} ä r e t t d e l r u m t i l l c_{0}$

Där definitionerna av c_0, M_nm och l^2 är följande: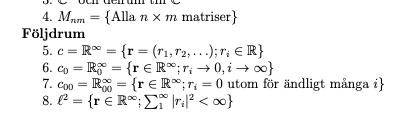

(1) gäller väl endast när n≤m? Kanske anses uppenbart men generellt sätt brukar dom vara noggranna med att skriva ut när så är fallet vilket dom inte gjort i det här häftet. Så vill kolla för att vara säker.

(2) att det här gäller är väl till följd av t.ex harmoniska serien? Det finns flera serier som går mot noll men som inte är konvergenta och därför är det ett hårdare krav för l^2 jämfört med c_0?

Vänligen,

Tycker du verkar tänka rätt på 2. Det är en del för att en följd måste gå mot 0 för att summan ska kunna vara konvergent, men det räcker inte. Just harmoniska serien blir väl konvergent här när det är upphöjt till 2, men ta roten ur varje tal så får du tillbaka poängen ;)

Haha just det... Men okej då är jag inte helt ute och snurrar på (2) då i alla fall.

Hur är det med (1)?

För att (1) ska vara sann måste de två rummen ha samma grundmängd, dvs vi måste ha m=n. Du måste kontrollera slutenhet också

Jag tror inte att man behöver kräva att n=m. Däremot måste, precis som Ygolopot säger, $n \leq m$ . M_nm innehåller ett gäng ickekvadratiska matriser som egentligen inte är relevanta för själva påståendet om symmetriska nxn-matriser.

Peter skrev:
Jag tror inte att man behöver kräva att n=m. Däremot måste, precis som Ygolopot säger, $n \leq m$ . M_nm innehåller ett gäng ickekvadratiska matriser som egentligen inte är relevanta för själva påståendet om symmetriska nxn-matriser.

Det beror på hur petig man vill vara. Rent stringent innehåller inte $M_{n m}$ en enda kvadratisk matris om inte n är lika med m. Däremot kan man visa att mängden av symmetriska matriser är isomorft med ett underrum av $M_{n m}$ men det är inte samma sak som att det är ett underrum.

Edit: Om du tillämpar definition 1.3 från din litteratur ser du att ett krav är att delrummet U är en delmängd till vektorrummet V. Jag tror att det är feltryck i kurslitteraturen(de brukar vara noggranna med sådana detaljer vad jag minns) och det borde stå att det är ett delrum av $M_{n n}$

Hej Ygolopot,

1. Mängden $M_{nm}$ består av alla matriser med n stycken rader och m stycken kolumner; det krävs inte av matriserna att de ska ha fler kolumner än rader.

Mängden av alla symmetriska matriser är trivialt en delmängd till $M_{nm}$ ; att det även är ett underrum kräver litet arbete att visa.

2. Det stämmer att mängden $l^2$ är en äkta delmängd till mängden $c_0$ som ju innehåller den divergenta harmoniska serien och alla multipler av den harmoniska serien.

Tack för svaren allihopa, precis som du är inne på Parveln så är det ett feltryck. Vår lärare har gått ut nu och rättat häftet och sagt att det egentligen ska stå $M_{n n}$ och inte $M_{n m}$ (precis som du trodde). Så hänger med lite bättre nu på vad som händer :)

Svara Avbryt

Visa senaste svar