Linjär algebra

Du kan utgå från punkten D och gå i normalens riktning till punkten 

P = D + n*t

För ett t-värde så kommer P att ligga i planet.

Jag brukar använda ortogonal projektion:

sökta avståndet är $s=| \overline{QD} |$ (blå vektor). Det kan uttryckas som

$s=| \overline{PD}\bullet \mathbf{n}_e |$  (vi projicerar magentafärgad vektor på normalen, P är en punkt i planet).

Notera: $\mathbf{n}_e$ (röd vektor) är enhets-normalvektor. (Normera $\mathbf{n}$).

Notera att mitt senaste inlägg resonerar kring problemet ”avstånd punkt-plan”. 

Ditt specifika problem berör hur punkten Q ( i min figur) ska väljas. Där följer du Dr. G:s tips.

Hur vet jag att enhetsvektorn är ortogonal mot planet? De illustrerar detta i boken och då ska avståndet vara:$$\begin{gathered} d=\left|\left(\overrightarrow{e}\overline{)\overrightarrow{PD}}\right)\right|=\left|Ax+By+Cz-D\right| då \left|\overrightarrow{e}\right|=1 \\ alt: \\ d=\left|\left(\overrightarrow{n}\overline{)\overrightarrow{PD}}\right)\right|=\frac{\left|Ax+By+Cz-D\right|}{\sqrt{A^2+B^2+C^2}} \end{gathered}$$

Men kör fast på enhetsvektor/ normalvektorn, hur får jag fram dess värden? 

Tidigare skrev du

” Jag får fram ett plan av de förstnämnda (tre) punkterna, men sedan vet jag inte hur jag ska fortsätta.”

Kan du presentera planets ekvation?

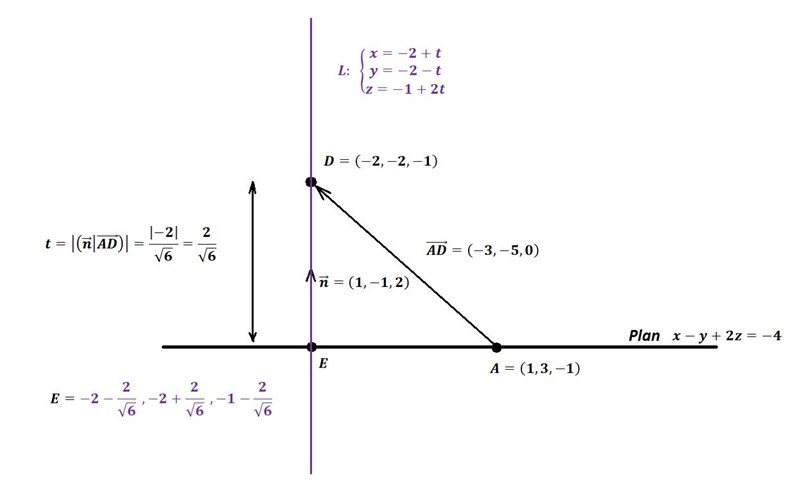
Sträckan värkar stämma enligt geogebra, men punkten $E$stämmer inte med facit, geogebra eller mitt svar.....

Svaret i facit är: $E=\left(1,-1,1\right)$

(1,1,0) ligger inte i planet 

x - y + 2z = -4

Utan att kontrollräkna fick jag en ekvation för planet till

3x + y + 2z = 4

Jag får fortfarande inte fram den sökta punkten, jag har nu $L\left\{\begin{array}{l}x=-2+3t\\ y=-2+1t\\ z=-1+2t\end{array}\right.$och sätter $t=\sqrt{14} (avståndet från planet \& den sökta punkten)$

och får:

$$\begin{gathered} x=-2+3\sqrt{14} \\ y=-2+\sqrt{14} \\ z=-1+2\sqrt{14} \end{gathered}$$

Vilket inte ger den sökta punkten....

D = (-2,-2,1)

Vi rör oss i normalens riktning (3,1,2) från D till P

P = D + n*t = (3t - 2, t - 2, 2t + 1)

P ska uppfylla planets ekvation

x + 3y + 2z = 4

ger t = 5/7

så 

P = (1/7, -9/7, 17/7)

Jag förstår fortfarande inte ditt resonemang, svaret ska bli $\left(1,-1,1\right)$

Avståndet $s=\sqrt{14}$ är korrekt.

Planets ekvation: Dr. G har rätt: $3x+y+2z-4=0$.

Normalens ekvation:

Insättning i planets ekvation (skärningspunkt normal-plan) ger att $t=1$ och den efterfrågade punkten Q (i min figur): $Q:(1, -1, 1)$, och efter kontroll:

vilket ger (mina beteckningar enl min figur): $|\overline{QD}|=\sqrt{14}$, som förväntat.

Aha, jag trodde att D = (-2,-2,1), men ser nu att D = (-2,-2,-1).

Då kanske det blir lite snyggare värden...

Tack!