Linjär Algebra, Vektorer och punkter
Jag har stött på en fråga som där de vill att jag ska få fram om en fjärde punkt S ligger i en triangel som utgörs av tre punkter PQR.
P=(2,3,3) Q=(5,4,7) R=(-1,8,5) S=(1,7,6)
PQ=(3,1,4) PR=(-3,5,2) RQ=(6,-4,2)
PS=(-1,-10,3) RS=(2,-15,1) QS=(-4,-11,-1)
Jag gissar påatt jag antingen ska använda Kryssprodukt eller eventuellt något med planets ekvation vilket jag har fått fram blir: -x-y+z=(-2)
Tack.
Finns det några sådana att ekvationen blir uppfylld? Då ligger S i planet.
I så fall, vad måste vidare gälla för α och β för att S skall ligga i triangeln?
PATENTERAMERA skrev:Finns det några sådana att ekvationen blir uppfylld? Då ligger S i planet.
I så fall, vad måste vidare gälla för α och β för att S skall ligga i triangeln?
Jag har redan fått fram att S ligger i planet genom att sätta in den i planets ekvation.
Sedan så vet jag inte vad det är som definierar att en punkt är inne i en triangel i samma plan så jag vet inte vad som gäller för a och b.
Philipbja skrev:PATENTERAMERA skrev:Finns det några sådana att ekvationen blir uppfylld? Då ligger S i planet.
I så fall, vad måste vidare gälla för α och β för att S skall ligga i triangeln?
Jag har redan fått fram att S ligger i planet genom att sätta in den i planets ekvation.
Sedan så vet jag inte vad det är som definierar att en punkt är inne i en triangel i samma plan så jag vet inte vad som gäller för a och b.
Om du räknar ut så borde det vara så att S ligger i triangeln om och .
Rita en figur och använd lite matematisk/geometrisk intuition.
PATENTERAMERA skrev:
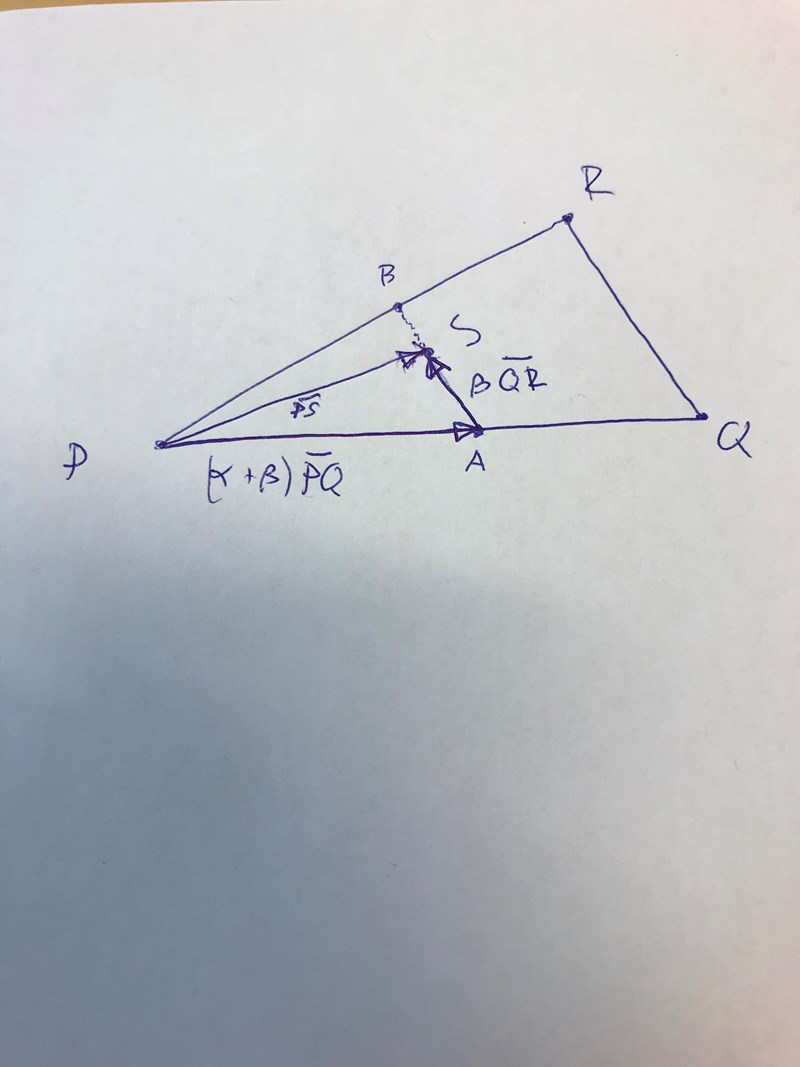
Låt oss anta att vi har hittat värden på , sådana att
Vi kan nu skriva om detta uttryck med hjälp av de Chasles relation
Genom att betrakta geometrin i figuren ovan inses att ett krav för att S skall ligga i triangeln är att
(1), vi antar i det följande att detta är uppfyllt.
Det inses vidare att ett ytterligare krav är
(2).
Likformformiga trianglar ger oss vidare att
.
Olikheten (2) kan därför skrivas
, och vi noterar vidare att
Således kan vi sammanfatta det hela så att S ligger i triangeln om QED