Linjär differensekvation av ordning 2 - varifrån får facit den homogena lösningen?
Halloj!
Jag sitter med följande gamla tentafråga:
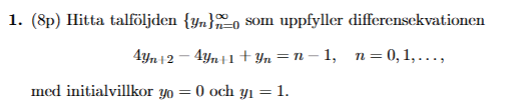
Jag började med att försöka hitta den homogena lösningen genom att ansätta . Jag kom då fram till den karaktäristiska ekvationen:
Vilket har lösningen .
Ur detta drar jag slutsatsen att lösningens homogena del måste vara:
för någon konstant .
I facit påstår de däremot att:

Varifrån får de faktorn ?
Det beror på att är en dubbelrot till karakteristiska ekvationen, så homogena lösningen bildar ett tvådimensionellt underrum i rummet av alla talföljder.
Om man hade en tredje ordningens differensekvation vars karakteristiska ekvationen hade en trippelrot , så skulle den homogena lösningen bli , och därmed skulle homogena lösningar bilda ett tredimensionellt underrum.
Något liknande händer när man arbetar med differentialekvationer där karakteristiska ekvationer har rötter med högre multiplicitet. Där blir homogena lösningen en exponentialfunktion multiplicerad med ett polynom vars gradtal beror på rotens multiplicitet.
Eller har jag missuppfattat din fråga och du undrar snarare om varför det just är som gäller när differensekvationens K.E. får roten med högre multiplicitet (där polynomets gradtal = multiplicitet - 1) ?
Ja precis, jag undrar hur man ska veta att man ska multiplicera med just polynomet . Det måste ju gå att härleda eller lista ut på något sätt, men jag vet inte hur.
Såg i mina föreläsningsanteckningar att jag hade noterat detta under en föreläsning men då stod det bara uppskrivet som en sats utan bevis.
Tillägg: 24 maj 2025 19:31
Och jag hänger inte riktigt med på kopplingen mellan rum och underrum och differensekvationer. I min hjärna existerar dessa begrepp inte ens närheten av varandra, men tydligen finns det någon koppling...
Låt oss fokusera på din konkreta homogena differensekvation vars KE har dubbelroten .
Man gör ansats , där sökes. När man sätter in detta i differensekvationen, förkortar och skriver på samma bråkstreck, så får man
för alla .
Man ser alltså att differensen mellan två intilligande element i talföljden är konstant. Med andra ord är en aritmetisk talföljd. (Aritmetiska talföljder kännetecknas av att differensen mellan intilliggande element är konstant.) För aritmetiska talföljder är den allmänna termen . Om man döper om till och till , så har man precis motiverat att
Resonnemanget ovan går att generalisera till godtyckliga differensekvationer, men man skulle behöva gräva sig ner i flera tekniska detaljer.
Ah, då är jag med! :)
Tack så mycket!


