Lös ekvationen (Matematik/Universitet)

Prova att gissa en rot och faktorisera mha. polynomdivision.

Annan metod:

$3x^3 - 6x + x^2 - 2 = 0$
$3x(x^2-2) + x^2 - 2 = 0$
$(3x+1)(x^2 - 2) = 0$
$(3x+1)(x + \sqrt{2})(x-\sqrt{2}) = 0$

statement skrev :
Prova att gissa en rot och faktorisera mha. polynomdivision.
Annan metod:
Error converting from LaTeX to MathML

Okej, hur bäst/smartast att tänka när man faktoriserar sådär?

heymel skrev :
statement skrev :
Prova att gissa en rot och faktorisera mha. polynomdivision.
Annan metod:
Error converting from LaTeX to MathML
Okej, hur bäst/smartast att tänka när man faktoriserar sådär?

Har redigerat inlägget då det blev fel i renderingen av LaTeX koden. Se mitt inlägg ovan.

Hej kompis!

Så här kan man lösa!

Elin123 skrev :
Hej kompis!
Så här kan man lösa!

Vad gulligt :D

men hur ska man tänka när man bryter ut sådär? Alltså hur ska man veta vilken grad som ska brytas ut??

heymel skrev : vad menar du med grad? :)

Elin123 skrev :
Hej kompis!
Så här kan man lösa!
Vad gulligt :D

men hur ska man tänka när man bryter ut sådär? Alltså hur ska man veta vilken grad som ska brytas ut??

Elin123 skrev :
heymel skrev : vad menar du med grad? :)
Elin123 skrev :
Hej kompis!
Så här kan man lösa!
Vad gulligt :D

men hur ska man tänka när man bryter ut sådär? Alltså hur ska man veta vilken grad som ska brytas ut??

Alltså rent allmänt, hur ska man tänka för att veta vilken grad man ska bryta ut? Är det grad-1 always? eller??

Det finns ingen standardmetod för det såvitt jag vet, utan det är mer en fråga om att ha löst tillräckligt många problem av den arten så att man känner igen och kan hitta mönster och samband.

Den här delen av matematiken är lite som ett hantverk, man får lära sig efter hand.

Jämförelse: Det finns ingen färdig ritning för hur man ska ta sig an arbetet med att platsbygga en bokhylla.

Yngve skrev :
Det finns ingen standardmetod för det såvitt jag vet, utan det är mer en fråga om att ha löst tillräckligt många problem av den arten så att man känner igen och kan hitta mönster och samband.
Den här delen av matematiken är lite som ett hantverk, man får lära sig efter hand.
Jämförelse: Det finns ingen färdig ritning för hur man ska ta sig an arbetet med att platsbygga en bokhylla.

Jo vet inte om jag riktigt håller med om det? eller menar du allmänt? för en andragradera (utan att veta pq) så går det ju)

tex: x^2+8x+12=0

brukar jag tänka: ngt+ngt =8.. samma ngt*ngt=12, vad finns det då för möjligheter å pröva mig framåt så. å då ser jag att det enda blir då (x-6)(x-2)..

Dessusom så kan man också använda p/q grejen, rationell rote? Så p dela konstanttermen och q dela högstagradskoefficienten och använda liggande stolen?

För nu när jag läser en annan ex: så säger dom att ev rötter kan vara (då till denna) är :

+- 1, +- 1/3, +- 2, +- 2/3

hur har de fått ut 1, 1/3(ok det såg jag ju att Elin hade faktoriserat ut där i bilden hon bifogade) samt 2. tyckte hon skrev sqrt(2).

Ytterligare hantverksknep:

Man bör alltid se om det finns någon enkel rot att "gissa". T.ex. 0 eller 1.

Om $x_1, x_2, x_3$ är rötter till $x^3+rx^2+sx+t=0$ gäller:

En snäll tredjegradsekvation har ofta två rötter som ligger symmetriskt, dvs $x_1=-x_2$

Om detta gäller för ekvationen är $x_3=-r$ en lösning (enligt samband 1) och bör därför ingå i det första man "testar" tillsammans med de enkla rötterna.

I vårt fall är $x_3=-r=-\frac{1}{3}$ och är en lösning! Detta insatt i samband tre ger omedelbart $x_{12}\pm\sqrt{2}$

Guggle skrev :
Ytterligare hantverksknep:
Man bör alltid se om det finns någon enkel rot att "gissa". T.ex. 0 eller 1.
Om $x_1, x_2, x_3$ är rötter till $x^3+rx^2+sx+t=0$ gäller:
Error converting from LaTeX to MathML
En snäll tredjegradsekvation har ofta två rötter som ligger symmetriskt, dvs $x_1=-x_2$
Om detta gäller för ekvationen är $x_3=-r$$ en lösning (samband 1) och bör därför ingå i det första man "testar" tillsammans med de enkla rötterna.
I vårt fall är $x_1=-r=-\frac{1}{3}$ och är en lösning! Detta insatt i samband tre ger $x_{12}\pm\sqrt{2}$

Error converting from LaTeX to MathML vad ska det stå där?

För tredjegradsekvationer finns det faktiskt en analytisk lösningsmetod, kallad Cardanos formel., fast den är så komplicerad att den inte används i praktiken.

Jag har fortfarande inte riktigt förstått hur de kan gissa ut rötter? Är det ngn som kan förklara det? facit säger att de har gissat +-1 , +- 1/3 , -+ 2/3 , +- 2.

Hur ?????

1. Kolla om 0 är en lösning, d v s sätt in x = 0 i ekvationen och kolla om det stämmer.

2. Kolla om 1 är en lösning, d v s sätt in x = 1 i ekvationen och kolla om det stämmer.

3. Kolla om -1 är en lösning, d v s sätt in x = -1 i ekvationen och kolla om det stämmer.

4. Kolla om 2 är en lösning, d v s sätt in x = 2 i ekvationen och kolla om det stämmer.

5. Kolla om -2 är en lösning, d v s sätt in x = -2 i ekvationen och kolla om det stämmer.

Eftersom ekvationen i din uppgift har en trea framför kvadrattermen, verkar det inte alltför långsökt att kolla med tredjedelar också.

När (om!) du hittar en lösning, kan du dividera ursprungsekvationen med (x-roten) och få en enklare ekvation - om det blir en andragradsekvation kan du ju lösa den med pq-formeln.

smaragdalena skrev :
1. Kolla om 0 är en lösning, d v s sätt in x = 0 i ekvationen och kolla om det stämmer.
2. Kolla om 1 är en lösning, d v s sätt in x = 1 i ekvationen och kolla om det stämmer.
3. Kolla om -1 är en lösning, d v s sätt in x = -1 i ekvationen och kolla om det stämmer.
4. Kolla om 2 är en lösning, d v s sätt in x = 2 i ekvationen och kolla om det stämmer.
5. Kolla om -2 är en lösning, d v s sätt in x = -2 i ekvationen och kolla om det stämmer.
Eftersom ekvationen i din uppgift har en trea framför kvadrattermen, verkar det inte alltför långsökt att kolla med tredjedelar också.
När (om!) du hittar en lösning, kan du dividera ursprungsekvationen med (x-roten) och få en enklare ekvation - om det blir en andragradsekvation kan du ju lösa den med pq-formeln.

Ja men det kan ju ta hur lång tid som helst? att pröva sig fram

Inte om du begränsar dig till till exempel 0, +/-1, +/-2 och +/- 3.

Om det ska finnas en rot långt bort från origo så måste antingen koefficienten framför x^3.termen vara väldigt liten eller koefficienterna framför x^2/x^1/konstanttermen vara väldigt stora.

Varför är det så tror du?

Yngve skrev :

Inte om du begränsar dig till till exempel 0, +/-1, +/-2 och +/- 3.
Om det ska finnas en rot långt bort från origo så måste antingen koefficienten framför x^3.termen vara väldigt liten eller koefficienterna framför x^2/x^1/konstanttermen vara väldigt stora.
Varför är det så tror du?

spännande : jag vet inte.

jag kan ju tycka att det kanske känns himla långsökt att sitta å leta efter bråktal och irrationella tal

Ärligt talat: Finns det en rot som inte är ett reellt tal så bör du använda "The Rational Root Theorem". d.v.s., OM det finns en rot som är ett rationellt tal så kommer du hitta den med rationella rotteoremet.

Då slipper du som ovan "gissa" första rötterna (vem gissar -2/3?). Du får i alla fall fram ett par rötter och en är just 2/3.

https://en.wikipedia.org/wiki/Rational_root_theorem

woozah skrev :
Ärligt talat: Finns det en rot som inte är ett reellt tal så bör du använda "The Rational Root Theorem". d.v.s., OM det finns en rot som är ett rationellt tal så kommer du hitta den med rationella rotteoremet.
Då slipper du som ovan "gissa" första rötterna (vem gissar -2/3?). Du får i alla fall fram ett par rötter och en är just 2/3.

https://en.wikipedia.org/wiki/Rational_root_theorem

Men den roten stämmer ju inte? så då fungerar inte alltid den beviset?

Jag håller med om att det kan vara lite långsökt att leta rötter utanför heltalen, men om du läser Guggles tips ovan så ger det lite ledtrådar kring vilka bråktal man skulle kunna pröva.

Angående varför koefficienterna måste vara beskaffade just på det sättet för att det ska finnas rötter långt från origo så kan man fundera på hur tredjegradspolynomets värde beror på avståndet från origo.

Eftersom det finns en x^3-term så kommer den att dominera hela polynomets värde om man kommer tillräckligt långt från origo.

I fallet positiv koefficient på x^3-termen så kommer ju grafen "nerifrån" vid stora negativa värden på x, passerar x-axeln på 1 eller 3 ställen innan den sticker iväg "uppåt" vid stora positiva värden på x.

I fallet negativ koefficient på x^3-termen så är det tvärtom, grafen kommer "uppifrån" vid stora negativa värden på x, passerar x-axeln på 1 eller 3 ställen innan den sticker iväg "nedåt" vid stora positiva värden på x.

Dessa x-axelpassager (nollställena) sker ju alltid där x^2, x^1 och konstanttermen i polynomet är precis lika stora men med motsatt tecken, som x^3-termen.

Eftersom x^3-termen till beloppet blir väldigt stor långt från origo så krävs alltså antingen en väldigt liten koefficient framför den eller stora koefficienter framför x^2, x^1 och konstanttermen för att dessa ska balansera x^3-termen och summan ska bli 0 (nollställe).

Ser du det framför dig?

heymel skrev :
woozah skrev :
Ärligt talat: Finns det en rot som inte är ett reellt tal så bör du använda "The Rational Root Theorem". d.v.s., OM det finns en rot som är ett rationellt tal så kommer du hitta den med rationella rotteoremet.
Då slipper du som ovan "gissa" första rötterna (vem gissar -2/3?). Du får i alla fall fram ett par rötter och en är just 2/3.

https://en.wikipedia.org/wiki/Rational_root_theorem
Men den roten stämmer ju inte? så då fungerar inte alltid den beviset?

Jo, det stämmer alltid. Du hade hittat -1/3 och sedan kunnat förenkla ditt polynom. Det var bara jag som fick för mig 2/3 och inte 1/3.

Man kan också försöka läsa länken jag gav dig så hade du själv kunnat utföra processen för att se vilka rationella rötter som är rimlig. :)

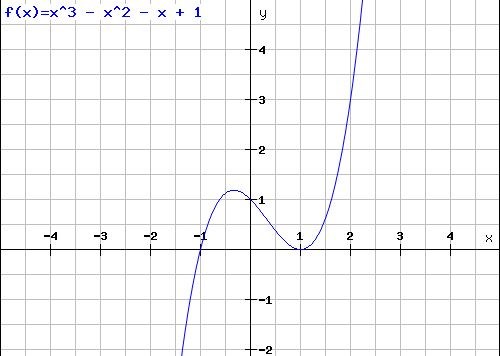
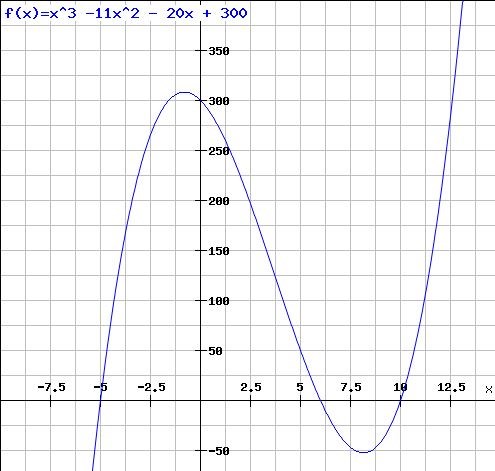
Här är två exempel på tredjegradskurvor.

Koefficienter nära 1 -> nollställen nära origo.

Stora koefficienter -> nollställen långt ifrån origo (i detta fallet vid -5, 6 och 10).

Hej!

Frågan som Heymel ställde var: Hur kan man smartast hitta roten till tredjegradspolynomet $3x^3+x^2-6x-2$ ?

Svaret på frågan är: Det finns inget svar på den frågan; det finns ingen metod som är smartast av alla tänkbara metoder.

Av de här föreslagna metoderna är det den som Elin123 föreslår som är smartast (enligt min mening); den utnyttjar polynomets struktur till fullo.

Om du vill ha en metod som fungerar för alla tredjegradspolynom så är det Cardanos formel som gäller (denna är P-Q-formelns komplicerade motsvarighet för tredjegradspolynom).
Om du vill ha en metod som söker efter rationella rötter till tredjegradspolynom med heltalskoefficienter så är det Rational Root Theorem som gäller. Om polynomet saknar rationella rötter så fungerar inte denna metod; du måste alltså veta på förhand att polynomet har en rationell rot.
Om du vill ha en metod som fungerar för just detta polynom så är det Elin123:s metod som gäller.

Albiki

... eller den metod som statement beskrev i första svaret.

woozah skrev :
Ärligt talat: Finns det en rot som inte är ett reellt tal så bör du använda "The Rational Root Theorem". d.v.s., OM det finns en rot som är ett rationellt tal så kommer du hitta den med rationella rotteoremet.
Då slipper du som ovan "gissa" första rötterna (vem gissar -2/3?). Du får i alla fall fram ett par rötter och en är just 2/3.

https://en.wikipedia.org/wiki/Rational_root_theorem

vi tar ett annat ex. https://www.pixeltopic.com/image/vgvprypphugmri/

jag är helt med på att man använder rational_root_theorem. Men då får vi ju bara +- 1(eftersom 5/5=1)?

Hur har man förstått att de ska bli 1/5 eller 5? vad motsvarar dom? P/Q

heymel skrev :
vi tar ett annat ex. https://www.pixeltopic.com/image/vgvprypphugmri/

jag är helt med på att man använder rational_root_theorem. Men då får vi ju bara +- 1(eftersom 5/5=1)?
Hur har man förstått att de ska bli 1/5 eller 5? vad motsvarar dom? P/Q

Teoremet säger att om det finns en rationell rot a/b så måste a dela konstanttermen (5) och b dela tredjegradskoefficienten (5). Eftersom de enda heltal som delar 5 är 1 och 5 så gäller det att:

Om a delar 5 så måste a vara lika med 1 eller 5.
Om b delar 5 så måste b vara lika med 1 eller 5.

Det ger endast 4 möjliga kombinationer av a och b, nämligen 1/1, 1/5, 5/1 och 5/5.

Två av dessa fyra är identiska så det finns endast tre olika möjliga rationella rötter, nämligen 1/5, 1 eller 5.

Var det svar på frågan?

Återigen använd sambanden mellan rötterna, -r=1/5 visar sig vara en rot, alltså är de andra rötterna:

$\frac{1}{5}x_{23}^2=t=1$

$x_{23}=\pm\sqrt{5}$

Yngve skrev :
heymel skrev :
vi tar ett annat ex. https://www.pixeltopic.com/image/vgvprypphugmri/

jag är helt med på att man använder rational_root_theorem. Men då får vi ju bara +- 1(eftersom 5/5=1)?
Hur har man förstått att de ska bli 1/5 eller 5? vad motsvarar dom? P/Q
Teoremet säger att om det finns en rationell rot a/b så måste a dela konstanttermen (5) och b dela tredjegradskoefficienten (5). Eftersom de enda heltal som delar 5 är 1 och 5 så gäller det att:
Om a delar 5 så måste a vara lika med 1 eller 5.
Om b delar 5 så måste b vara lika med 1 eller 5.
Det ger endast 4 möjliga kombinationer av a och b, nämligen 1/1, 1/5, 5/1 och 5/5.
Två av dessa fyra är identiska så det finns endast tre olika möjliga rationella rötter, nämligen 1/5, 1 eller 5.
Var det svar på frågan?

Kan testa med ett annat tal? denna: 2x^3-x^2-10x+5=0

p/q =5/2?? och de enda som kan dela dom är.. 1?? 1/2 och 5?

heymel skrev :
Kan testa med ett annat tal? denna: 2x^3-x^2-10x+5=0
p/q =5/2?? och de enda som kan dela dom är.. 1?? 1/2 och 5?

Nej p/q är inte lika med 5/2.

Teoremet säger att OM det finns en rationell rot x = p/q till ekvationen så har den roten egenskapen att p delar konstanttermen 5 och q delar tredjegradskoefficienten 2.

Endast talen 1 och 5 delar 5, alltså måste p i så fall vara 1 eller 5.
Endast talen 1 och 2 delar 2, alltså måste q i så fall vara 1 eller 2.

Det ger följande möjliga rationella rötter p/q:

1/1, 1/2, 5/1, 5/2

Pröva dessa möjliga rötter i tur och ordning. Om ingen av den löser ekvationen så saknar ekvationen alltså rationella rötter.

Och den här gången är -r=1/2 varför de andra rötterna är $\frac{1}{2}x^2=t=5/2\qquad x=\pm\sqrt{5}$

Vilket sammanträffande att alla tre ekvationerna löses så enkelt direkt, nästan så man tror att de är specialanpassade...