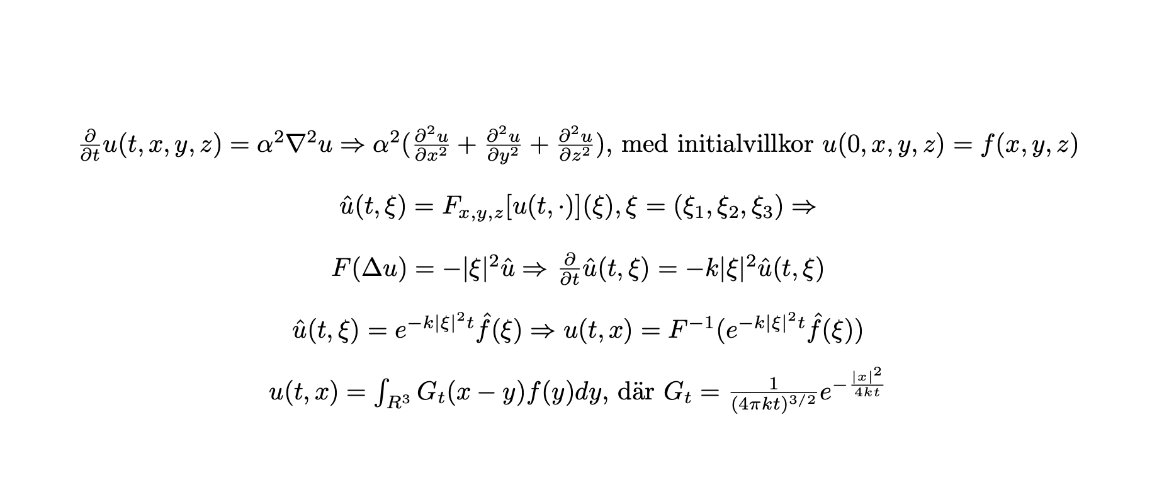Lösa värmeekvationen med variabelseparation
Hej!
Jag sitter med differentialekvationen nedan:
med initialvillkor
Jag började med att ansätta . Om vi sätter in detta i differentialekvationen erhåller vi:
Efter lösning av båda dessa ODEs separat fick jag:
Hur fortsätter man vidare härifrån? Har jag redan här kanske missat lösningar på och ?
Man brukat sätta konstanten = -λ,
så slipper man exponentiellt växande lösningar, vilka man inte ofta stöter på när det gäller värmeledning.
Okej, då kör jag på det istället!
Men hur skulle man ta sig vidare principiellt efter att vi har bestämt och som ovan? Har vi fångat alla lösningar redan?
Vad har du för intervall för x? Finns det några randvillkor?
Jag har inga randvillkor utan jag ville försöka lösa den så generellt som möjligt. Intervallet för kan vi väl låta vara .
Hmmm... Då är problemet otillräckligt specificerat. Det finns oändligt med lösningar beroende på vad (eller eventuellt ) gör vid respektive .
Önskar man sig att återuppfinna Fourierserier, så vill man ha homogena randvillkor, t.ex. eller eller någon blandning av dessa.
Om intervallet för bestod av hela reella tallinjen och man sökte en begränsad lösning , så kunde man uttrycka lösningen som faltning av och värmekärnan (heat kernel). Detta kan motiveras/härledas m.h.a. Fouriertransformen. (Det går att använda variabelseparation, men den behövs egentligen inte.)
Som LuMa påpekar är nästa naturliga steg att ansätta randvillkor och se vad man får för lösningar. Vi kan till exempel tänka oss att vi räknar på en homogen stav som är isolerad (inget flöde) i båda ändar, dvs
Jag tror det är lättare för dig att arbeta med lösningar på formen
Om du nu ansätter randvillkoret kommer och för att få något annat än för (vilket vore en tråkig lösning, vi är intresserade av icke-triviala icke-tråkiga lösningar) så får du ett kvar ett intressant krav samt en samling lösningar.
Fundera slutligen över ett giltigt initialvillkor , hur kan ett sådant se ut?
Kan det här ha något med Fourierserier att göra?
Hej, tack för alla svar!
Detta har inget med Fourier direkt att göra utan är för en kurs i Fourieranalys där vi måste hålla en presentation där vi ska presentera en motivering till varför man behöver Fouriertransformer. Vi tänkte ha med ett exempel där vi löser värmeekvationen med både variabelseparation och Fouriertransform och visar att det ena blir bra mycket jobbigare än det andra. Här är exemplet som min (mycket kunnigare än jag) kursare kokade ihop för den tredimensionella värmeekvationen:
Jag försöker lösa den endimensionella värmeekvationen med samma typ av villkor som han använde. Vad jag kan se hade han väl endast ett begynnelsevillkor och inget annat?
Ok, då är det nog som ger motsvarande endimensionellt problem. Säg att man söker en begränsad lösning till värmeledningsekvationen med begynnelsevillkoret , , (där är en kontinuerlig funktion sådan att )
Jag vill hellre ha i exponenten hos , så jag väljer att är den ena ODE:n och med samma är den andra ODE:n. (Detta är oväsentligt och bara en vanesak, men jag tycker man får snyggare uttryck på vägen.)
Nu ska man lösa ODE:erna. Börja med tidsfunktionen:
Man söker lösningar som är begränsade för . Detta kräver att . Man kan då tänka sig att för något reellt tal .
Nu tittar man på . Denna ekvation löses av
ifall
och
ifall . Eftersom en begränsad lösning sökes, så måste .
Man kan alltså säga att varje funktion skriven på formen med är en lösning till ODE:n .
Slutsats: Varje funktion , där och , uppfyller ekvationen
Varje superposition (d.v.s. linjär kombination) av med olika omegor också uppfyller PDE:n. Eftersom det finns ett kontinuum av omegor, så ges superpositionen inte av en ändlig summa med olika omegor, utan av en integral med omega som integrationsvariabeln:
Denna funktion också uppfyller PDE:n, vilket man inser genom att derivera m.a.p. x och t under integraltecknet. Det är inte alls trivialt att bevisa att man faktiskt får derivera innanför integralen, men låt oss vara optimister.
Frågan är vad som ska väljas som . Lösningen skall uppfylla begynnelsevillkoret , vilket ger sambandet:
d.v.s. skall vara inversfouriertransformen av eller snarare omvänt: skall vara fouriertransformen av . (Bortsett från eventuell normeringsfaktor eller .)
Man har alltså kommit fram till att
(Jag vet inte vilken variant av Fouriertransformen ni använder, så eventuell normeringsfaktorn eller kan behöva läggas till.)
Enligt räknelagarna för (invers)fouriertransformen får man att uttrycket i HL är helt enkelt faltning av med värmekärnan.
Lapplaceoperatorn har ett diskret spektrum på ett ändligt intervall och ett kontinuerligt spektrum på hela . Så i en mer generell mening är Fouriertransformen bara ett sätt att "diagonalisera" operatorn i det kontinuerliga fallet. Man kan säga att Fouriertransformen är den underliggande matematiska strukturen till värmeledningsekvationen när vi betraktar och kommer därför dyka upp som "delsteg" i en mer eller mindre förklädd form. Formellt säger man att Fouriertransformen realiserar spektralrepresentationen av Laplaceoperatorn på . Dvs, oavsett om man använder skalinvarians, variationsargument med energimetoder eller någon annan mer fysikinriktad lösningsmetod leder alla vägar till Rom.
BTW , hur långt har ni kommit i kursen? Fouriertransformer och faltning brukar ligga i den senare delen och är därmed lite olämpligt (tycker jag) att använda som motiverande exempel i början av kursen.
Men om ni redan börjar bli klara med kursen är det en annan femma :)
Tack för svaren! Ska sätta mig med detta senare ikväll.
Vi har precis påbörjat kursen men vår examinator tyckte att det lät som en bra idé att ta med. Det handlar bara om att lätt motivera varför Fouriertransformen är användbar, i detta fall endast genom att lösningen är ”kortare”. Ingen kan teorin än.