Lurig uppgift
Hej!
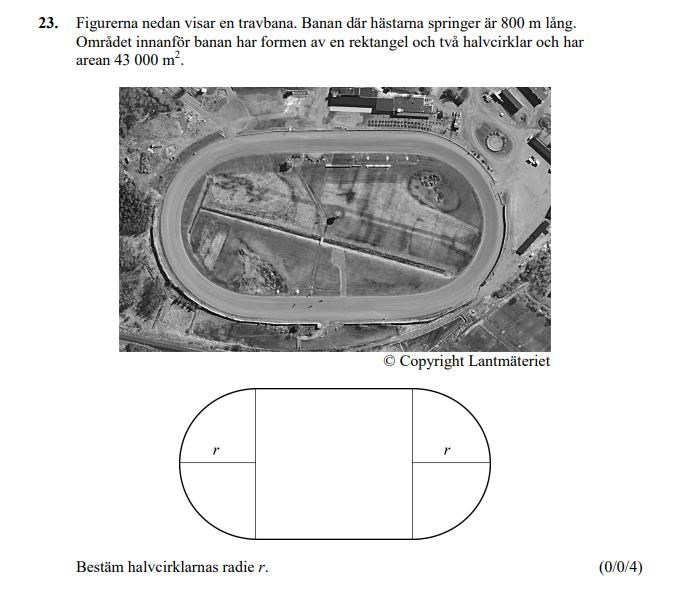
Någons lösning:

Den här uppgiften ger två värden för radien. När jag själv löste uppgiften tänkte jag att båda värden kanske skulle fungera. Men så var det tydligen inte. R kan tydligen inte vara 177 m. När man räknar på det är detta uppenbart, för om r = 177 så är omkretsen mycket större än banans längd vilket inte går. Jag är dock förvirrad, för jag kan inte förstå hur man kan få en falsk lösning på detta sätt när man ställt upp korrekta ekvationer. Hur kan en falsk rot bara uppstå ur intet? Särskilt när det är inte gäller variabler under några rottecken eller liknande för sådant hade jag kunnat begripa.
Tack på förhand.
När du blandar in andragradsekvationer kan det hända att det finns 2 rötter som överensstämmer med ekvationerna du har ställt upp, men att bara en av dem har en meningsfull tolkning i ditt scenario. I det här fallet är visserligen en lösning som uppfyller villkoren du har ställt upp, men den lösningen skulle också implicera att längden är negativ. Eftersom det i verkligheten inte finns några negativa avstånd, väljer vi alltså att bortse ifrån lösningen .
Toffelfabriken skrev:När du blandar in andragradsekvationer kan det hända att det finns 2 rötter som överensstämmer med ekvationerna du har ställt upp, men att bara en av dem har en meningsfull tolkning i ditt scenario. I det här fallet är visserligen en lösning som uppfyller villkoren du har ställt upp, men den lösningen skulle också implicera att längden är negativ. Eftersom det i verkligheten inte finns några negativa avstånd, väljer vi alltså att bortse ifrån lösningen .
Mycket tacksam för denna tydliga förklaring. Att x blev negativ hade jag inte beaktat innan, men det är logiskt.


