Maclaurinutveckling
Hej
kan någon hjälpa mig med att lösa följande uppgift:
Bestäm om
Jag tror att man kan utnyttja att om x är nära 0
Vad menar du med p_2(x)?
Att för x nära 0, följer av att 1 + x/2 är av . Så du kommer inte kunna använda det. Utan du har att
Så det är bara att räkna på. (Man kan använda Newtons binomial sats också).
Den utveckling som Stokastisk hänvisar till är följande. Den är mycket användbar då den täcker in många funktioner (olika parametervärden).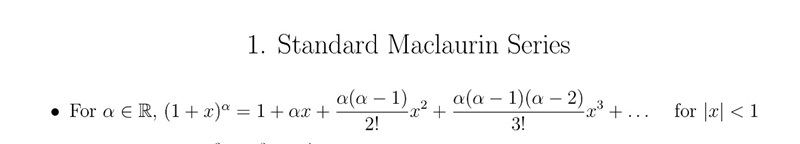
Om du menar Maclaurinutvecklingen upp till grad två vet du alltså att den är av typen
Koefficienten a kan du få fram med andraderivatan.
Hej B. N.!
Det hade varit bättre om du skrivit:
Bestäm Maclaurinpolynomet av grad 2 till funktionen .
Albiki
Hej!
Maclaurinpolynomet av grad 2 till funktionen är lika med
där koefficienterna och och bestäms av funktionen ; det ska gälla att
och att derivatorna
och .
Eftersom polynomet är sådant att och och så ser du att koefficienterna ges av och och .
För funktionen är och derivatorna och .
Albiki


