MaFy 2015, 7.
Hej!
Jag har en fråga angående dopplereffekt.
Jag fick fram att då källan rör sig bort från mottagaren med farten v_k har vi:
f' = f * ( v / v_k + v).
Räcker det att subtrahera istället för att addera i nämnaren om källan skulle röra mot mottagaren?

Den formeln du har gäller för en sändare i vila och en mottagare i rörelse (i förhållande till utbredningsmediet, luften).
De här formlerna hittade jag i min formelsamling (tryckt 1971 men jag tror den stämmer :-) ).
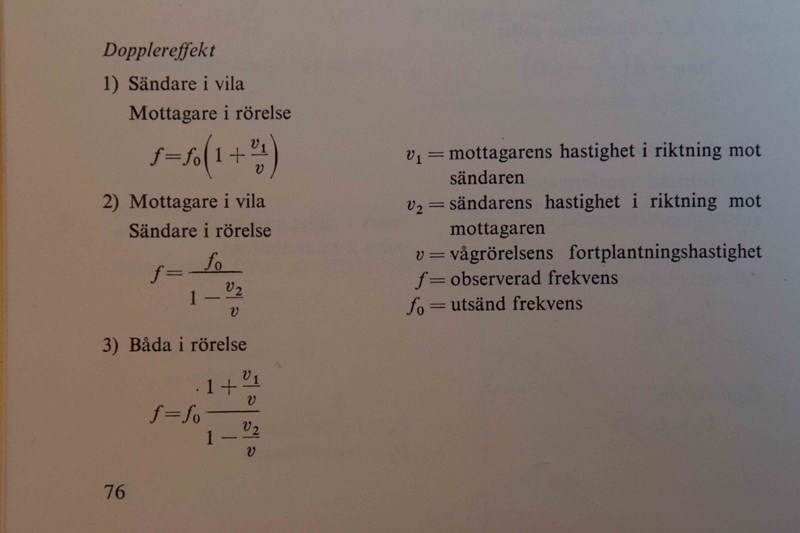
Formel 1 blir den som du har efter lite omstuvning, formel 2 är den som du ska använda.
ThomasN skrev:Den formeln du har gäller för en sändare i vila och en mottagare i rörelse (i förhållande till utbredningsmediet, luften).
De här formlerna hittade jag i min formelsamling (tryckt 1971 men jag tror den stämmer :-) ).
Formel 1 blir den som du har efter lite omstuvning, formel 2 är den som du ska använda.
Enligt https://www.pluggakuten.se/trad/vagor-7/ ges svaret av att lösa ut v_s ur 2 × v/v−v_s = v/v+v_s.
Frågan är varför det är (+) i högerledets nämnare. Kan någon förklara?
bump
Jag undrar om den är användbar i detta fallet. Den verkar härledd ur formel 3 med f = 2 x f0. Men i så fall har man inte samma v på höger och vänster sida om likhetstecknet. v1 skulle vara 0 eftersom mottagaren är stillastående i förhållande till luften och då blir den till formel 2.



