Mängdlära - definition för de reella talen utifrån Q
God middag!
Jag håller för tillfället på läsa in mig lite i elementär topologi och mängdlära. Just nu läser jag om hur de reella talen kan definieras utifrån de rationella talen. Först definieras en delmängd till som en "dedekind cut" om följande kriterier uppfylls för :
(c1) samt
(c2) Om exiterar alla också i
(c3) saknar ett maximum. Om finns det ett sådant att .
Sedan definieras mängden som mängden av alla "dedekind cuts". Nu har jag två frågor:
- Hur kan man definiera ett reellt tal som en mängd? Är alla reella tal egentligen mängder?
- Hur får man in tal som exempelvis i den definitionen?
På svenska säger vi oftast "Dedekind-snitt". Men det är viktigt att förstå vad som menas med snitt i detta sammanhang.
Ett snitt kan lite förenklat beskrivas som ett mängdpar så att
- och är disjunkta icke-tomma delmängder av där
- Om och följer att
Vidare säger man att är ett "hål" eller "gap" om saknar ett största element samtidigt som saknar ett minsta element.
Slutligen är ett snitt Dedekind eller ett "Dedekindsnitt" om saknar största element.
Av orsaker vi kan vänta med (t.ex. hur man definierar vad som menas med att en mängd är tät i en annan mängd samt varför vi egentligen inte får använda utan förbehåll) kan du lite förenklat se mängden som mängden rationella tal ) och du får lita på att det är omöjligt för att ha ett största element samtidigt som har ett minsta element.
Kvar finns två tänkbara typer av Dedekindsnitt, antingen är sådant att eller hål.
Du kan utan större begreppsmässig förvirring föreställa dig att talet du letar efter i någon mening ligger i (gränslandet mellan) , antingen som minsta element i (och då är talet rationellt) eller som ett irrationellt tal (hål).
Nu till det roliga, för att lära känna snitt och studera kan du börja med att ansätta
Visa att snittet är ett hål i de rationella talen .
Visa spoiler
Börja med att visa att A saknar ett största element.
Tack för ditt utförliga svar!
Jag håller på att försöka förstå allting. Men jag är lite fundersam kring kring kravet om att . Jag tror jag förstår själva principen, att man tar en mängd och delar upp den i två delar kring något värde som inte ingår i någon av delmängderna (förutom om vi kollar på den andra typen av Dedekindsnitt). Låt säga att vi betraktar:
Här skulle vi kunna skapa ett mängdpar :
samt
Dessa mängder är (i) disjunkta, (ii) delmängder av och (iii) alla element i är strikt större än i (om hela universumet utgörs av ).
Men det sista kravet om unionen av mängderna passar inte in här.
Kruxet är alltså att jag inte förstår hur man får med unionkravet när det alltid finns (minst?) ett element "mellan" mängderna som inte ingår.
I ditt exempel finns bara två möjliga snitt
Kommer mängden A innehålla ett största element i något av fallen? Vad var regeln för att få påstå att snittet är Dedekind?
Jag tror jag förstår vad du vill undersöka, men tänk på att din mängd inte har ett oändligt antal element. Mängden gör förmodligen inte heller anspråk på att "nå" alla element i t.ex. R.
Oj, jag uttryckte mig lite slarvigt i min fråga. Jag är med på att snittet inte kan utgöra ett Dedekindsnitt. Det jag menade var hur definitionen för ett hål passar ihop med att .
Om snittet ska vara ett hål vet vi att det saknas ett maximum för samt ett minimum för . Men vi vet att alla hål är snitt och att ett kriterium för att ens vara ett snitt är att .
Men om mängderna saknar maximum och minimum , för det kommer ju alltid saknas något element.
Men jag tror som sagt att jag förstår själva principen. Jag förstår det som att om Dedekindsnittet är ett hål så är det sökta talet hålet i sig och irrationellt, och rationellt om det istället ingår i .
naytte skrev:
Men jag tror som sagt att jag förstår själva principen. Jag förstår det som att om Dedekindsnittet är ett hål så är det sökta talet hålet i sig och irrationellt, och rationellt om det istället ingår i .
Just det!
Dock innebär det inte att det saknas något tal i . Tvärtom är det viktigt att alla element i grundmängden finns med, alltid.
Snittexemplet () jag gav är ett exempel där , alla rationella tal finns med, antingen i eller i . Trots det ligger det ett tal som inte hör till grundmängden i "hålet". Dvs finns av naturliga skäl varken i , eller .
Du får inte själv plocka bort något rationellt tal i samband med att du lägger ditt snitt så att .
För att till exempel snitta vid det rationella talet måste alltså en av olikheterna vara snäll och inkludera gränsen. Annars har du opererat bort ett rationellt tal. Är du med?
Ja, jag tror det. Så i ditt exempel med har vi alltså följande situation:
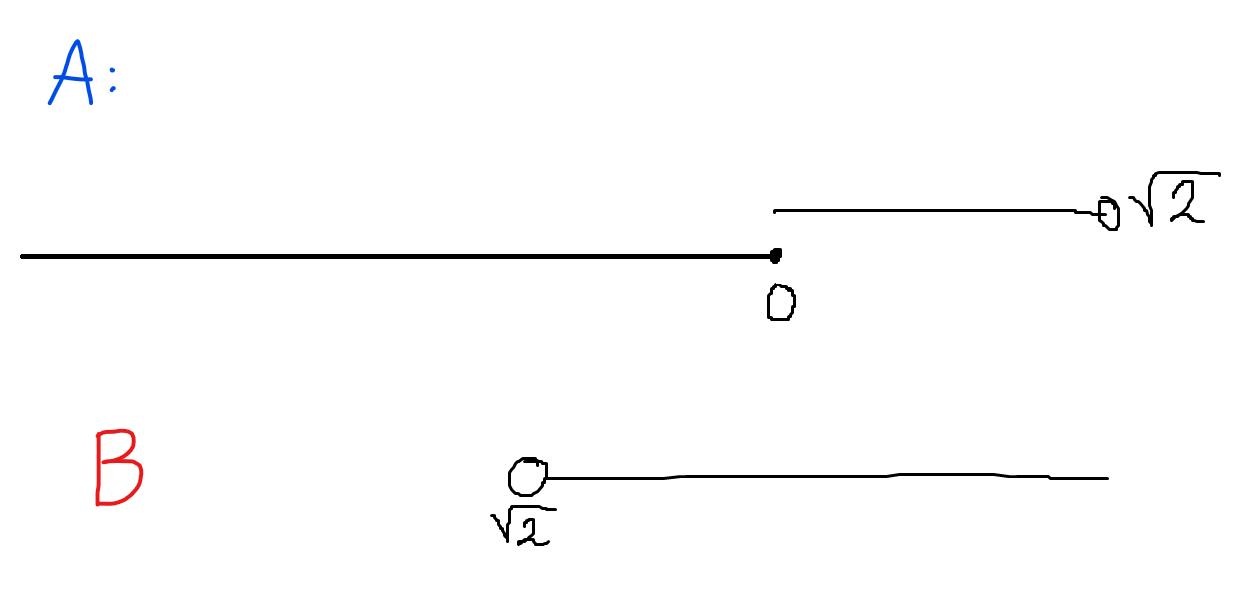
Och om man lägger ihop dessa får man:

Och definieras då som hålet som uppstår då man tar unionen?
Jag tittade exempelvis på denna video, där det påstods att tredje roten ur två kan definieras:
Och nu är jag helt lost. Hur kan man definiera ett tal som en mängd?
Jag förstår vad ett Dedekindsnitt är nu åtminstone. Men jag förstår inte hur ett tal kan definieras som ett snitt.
Eftersom mängderna och tillsammans ska bilda kan du om du får givet klura ut hur måste se ut. Därför anger man ibland bara vänstermängden.
Däremot vet jag av pedagogisk erfarenhet att det är lättare att tänka på Dedekindsnitt som snarare än som bara en ensam mängd.
Om du låter vänstermängden i ditt snitt (dvs ) vara mängden i frågan kan du alltså bestämma och sedan visa att är ett Dedekindsnitt, närmare bestämt ett hål i .
Okej.
Blir då?
Japp, och vidare är såklart , dvs de rationella talen.
Det kan kännas som att du "tagit bort" , men det har du inte eftersom talet inte fanns i från början.
Nu kan du visa att faktiskt är ett Dedekindsnitt, men det kräver en del arbete, bland annat ska man visa att saknar ett största element, vilket är lite omständligt om man ska göra det rigoröst.
Okej. Så definieras i detta fall som hålet ?
Ja, eller Dedekindsnittet
Okej, då är jag nog med!
Men var någonstans får man reda på att det rör sig om ett hål i definitionen från videon:
?
Och en annan sak:
hur vet man att hålet inte innefattar "fler tal"? Tänk om det finns fler irrationella tal i "hålet" än bara ?
Att i det här fallet är Dedekindsnitt av håltyp framkommer när man gör den fullständiga analysen av snittet .
Vidare kan man visa att varje reellt tal, oavsett om det är rationellt eller irrationellt, motsvarar ett och endast ett unikt Dedekindsnitt. Det beror på att man kan komma "godtyckligt nära" varje irrationellt tal och man säger att de rationella talen är täta i .
Kan man alltså komma godtyckligt nära varje irrationellt tal utan att stöta på ett annat irrationellt tal på vägen? Alltså, "omges" varje irrationellt tal alltid av rationella tal?
I exemplet med hade vi ju två mängder:
Så det kan alltså inte komma med något annat irrationellt tal i "vårt hål"? Hur kan man visa det?
Svar Ja I varje omgivning till ett reellt tal (alltså både irrationella och rationella) finns såväl rationella som irrationella tal.
Ska försöka återkomma med mer om detta, men hinner ej just nu.
För att precisera min fråga lite mer: det är ju naturligtvis för att är en "tät mängd". Om man accepterar det som ett faktum kan man enkelt visa att det bara kan finnas ett irrationellt tal "per hål". Men hur kan man visa att en mängd är tät?
Q är totalt ordnad av <. Det garanterar att mängderna a<x<b utgör en bas för en topologi, den s k ordningstopologin, som är lika med den vanliga topologin på Q. Det betyder att varje öppen mängd i Q kan erhållas som en union av basmängderna a<x<b. Den vanliga topologin har absolutbeloppet som metrik. Alltså kan man med den undersöka de konvergenta följderna i Q.
För att visa att en mängd S är tät i T måste man visa att varje omgivning till ett element i T innehåller ett element ur S. (En omgivning till ett element x är en mängd som innehåller en öppen mängd som innehåller x). Det kan man t ex göra genom att visa att det finns en följd i S som konvergerar mot ett givet element i T.
Det är intressant att Q är en äkta delmängd av R. Det har du redan sett ovan med . I det fallet är det lätt att hitta en olikhet för A-mängden med ett algebraiskt uttryck r2 t v om olikhetstecknet <. Ett annat exempel är emellertid följden 3, 3,1, 3,14, 3.141... som ju konvergerar mot mot det irrationella talet pi. Eftersom pi är transcendent så finns det faktiskt inte något algebraiskt uttryck att sätta t v om <. Det ställer till tekniska problem med Dedekind (som ju är den mest stringenta metoden) och gör de konvergenta följderna i Q intressanta. Notera också att Cauchys konvergensprincip gör det möjligt att avgöra om en följd i Q är konvergent UTAN att veta vart den konvergerar. Detta var ett mycket summariskt inlägg om topologin för Q och möjligheten att karaktärisera elementen i R med hjälp av konvergenta följder.
Okej, då är jag med!
Men jag har en fråga till. Jag såg på ett annat forum att vissa matematiker insisterar på att de (irrationella) reella talen definieras som Dedekindsnitten själva (alltså t.ex. som vänstermängden). Men här betraktar vi det ju som hålet som uppstår i snittet. Dr. Peyam i videon jag länkade ovan betraktade det som en mängd. Men jag har väldigt svårt att greppa det sättet. Hur kan:
""
vara ekvivalent med
" är hålet mellan mängderna "?
Jag är med på hur man kan betrakta det som ett hål mellan två mängder. Men hur kan man betrakta det som en mängd?
Det är inte ovanligt. Här ett annat exempel: (Jag har inte tillgång till symbolen för tomma mängden så jag får kalla den T) Betrakta följden T, {T,{T}}, {T, {T}, {T,{T}}}, , , Det är följden av de första ordinaltalen. Antalet element i den är 1, 2 , 3, o s v och står därför för mäktigheten. Den borde vara ett tal, men representeras av en mängd. I förstone verkar detta helt ointressant, men tänk att fortsätta den till oändligheten, och oändl är som bekant inte ett tal så nu blir det mer relevant. Detta ordinaltal kallas kardinaltalet för en uppräknelig oändlighet. Tar man ännu ett steg får man fortfarande bara en uppräknelig oändl men sviten av ordinaltal tar aldrig slut så någon gång kommer man till ett ordinaltal som inte är uppräkneligt och det ordinaltalet är då ett nytt kardinaltal ”kontinuets mäktighet”, R alltså. Ordinalerna har den fantastiska egenskapen att vara Välordnade, vilket betyder att varje delmängd har ett minsta element. Av vanliga kända mängder är det bara N som har den egenskapen, men alla mängder kan faktiskt välordnas. Allmänt när matematiska objekt företer samma struktur så talar man om att ett objekt kan Representera ett annat. Ett exempel är att en vektor kan ha en representant. Vektorn är ju egentligen en mängd lika långa ströckor med samma riktning.
En ordnad mängd är tät om om den har minst två element och om det för alla gäller att det finns så att .


