Mangoldt funktion

Jag begriper inte riktigt det ditt facit skriver. Hur kan de veta att $n$ är en primtalspotens? Kan du lägga upp en bild av lösningen så det kanske blir lite tydligare?

Själv tycker jag att det är fiffigare att resonera enligt följande:

Säg att $n$ har delare $d_1,d_2,...,d_{k_d}$. Då blir summan:

$\displaystyle\sum_{d|n}\Lambda\left(d\right)=\Lambda\left(d_1\right)+\Lambda\left(d_2\right)+...+\Lambda\left(d_{k_d}\right)$

Alla tal som inte är primtal eller primtalspotenser kommer att ha $\Lambda(d)=0$, och alltså blir vi endast kvar med summan av primtalsfaktoriseringens logaritmer (notera att primtalspotenser $p^k$ kommer att bli logaritmen av $p$ adderat $k$ gånger, d.v.s. samma sak som $\log(p^k)$). Om vi sedan säger att $n$ har primtalsfaktorer $p_1,p_2,...,p_{k_p}$ blir summan:

$\displaystyle\sum_{d|n}\Lambda\left(d\right)=\log\left(p_1\right)+\log\left(p_2\right)+...+\log\left(p_{k_p}\right)$

Med hjälp av en logaritmlag är det sedan hyfsat enkelt att se att detta blir $\log(n)$.

Svaret som jag har till exemplet är: 

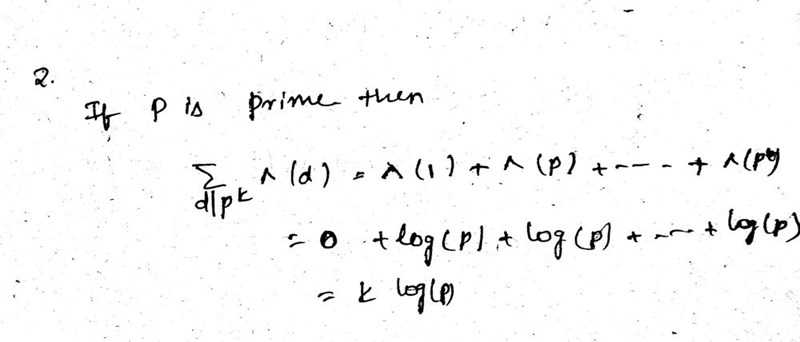
Okej, så här resonerar de:

De börjar med att visa att ifall $n=p^k$ (d.v.s. $n$ är en potens av ett primtal) så blir summan:

$\displaystyle\sum_{d|p^k}\Lambda\left(d\right)=\Lambda\left(1\right)+\Lambda\left(p\right)+\Lambda\left(p^2\right)+...+\Lambda\left(p^k\right)=$

$=0+\log(p)+\log(p)+...+\log(p)=k\log(p)$

eftersom delarna till $p^k$ endast är potenserna av $p$ med exponent upp till och med $k$. Detta faktum är användbart för att visa det för alla naturliga tal $n$, eftersom alla $n$ går att faktorisera till primtalspotenser (enligt aritmetikens fundamentalsats). Alltså, om vi tar ett naturligt tal $n$ med primtalsfaktoriseringen:

$n=p_1^{k_1}\cdot...\cdot p_{\gamma}^{k_{\gamma}}$

kan vi dela upp summan av mangoldtfunktionen av dess delare till summan av primtalspotenser (vilket vi började med att bevisa). Alltså,

$\displaystyle\sum_{d|n}\Lambda\left(d\right)=\sum_{i=1}^{\gamma}(\sum_{d|p_i^{k_i}}\Lambda\left(d\right))=$

Den inre summan blir ju helt enkelt det vi började med att bevisa, d.v.s. $k\log(p)$:

$=\displaystyle\sum_{i=1}^{\gamma}k_i\log\left(p_i\right)=$

Och det är inte så svårt att visa att detta blir:

$=\displaystyle\sum_{i=1}^{\gamma}\log\left(p_i^{k_i}\right)=\log\left(p_1^{k_1}\right)+...+\log\left(p_{\gamma}^{k_{\gamma}}\right)=\log\left(p_1^{k_1}\cdot...\cdot p_{\gamma}^{k_{\gamma}}\right)=\log\left(n\right)$

Sedan behöver man bara applicera Möbius inversionsformel.

okej men jag är inte med på hur man får det första steget dvs $\sum _{d|{\rho }^k}\wedge \left(d\right)=\wedge \left(1\right)\wedge \left(\rho \right)+\wedge \left({\rho }^2\right)+...+\wedge \left({\rho }^k\right)=0+\log \left(\rho \right)+\log \left(\rho \right)+...+\log \left(\rho \right)=k\log \left(\rho \right)$ och hur detta ger oss $n={\rho }_1^{k1}...{\rho }_{\gamma }^{k\gamma }$

Delarna till en primtalspotens är ju bara potenser av primtalen. Exempelvis är delare till $3^3$ $3^0,3^1,3^2,3^3$. Det är du med på, eller hur?

Eftersom delarna till primtalspotensen $p^k$ är $p^0,p^1,...,p^k$ blir summan:

$\displaystyle\sum_{d|p^k}\Lambda\left(d\right)=\Lambda\left(1\right)+\Lambda\left(p\right)+...+\Lambda\left(p^k\right)$

Enligt definitionen till Mangoldtfunktionen är $\Lambda\left(1\right)=0$ och för övriga potenser får vi bara $\log(p)$. Alltså blir summan:

$\displaystyle\sum_{d|p^k}\Lambda\left(d\right)=0+\log\left(p\right)+...+\log\left(p\right)=k\log\left(p\right)$

Notera att detta bara är ett delsteg i beviset som kommer till användning senare (man brukar kalla det för ett lemma). Efter att man visat detta börjar man på det "riktiga" beviset där ovanstående används.

Enligt aritmetikens fundamentalsats kan alla naturliga tal skrivas som en unik produkt av primtalspotenser. Detta är inget som vi bevisar, utan det är något som vi antar är sant. Exempelvis är $18=2\cdot3^2$, och man kan göra på liknande sätt för alla naturliga tal. Detta är anledningen till att vi kan skriva:

$n=p_1^{k_1}\cdot...\cdot p_{\gamma}^{k_{\gamma}}$

Eftersom vi redan visat vad summan blir för en primtalspotens kan vi bara dela upp $n$ i dess primtalspotenser ($\gamma$ stycken) och räkna utifrån det.