Måste en integral innehålla en differentialoperator?

God (väldigt tidig) morgon, Pluggakuten!

Jag har befattat mig lite med integraler på senaste och jag stötte nyligen på en uppgift där man behövde vara lite kreativ. Man skulle bestämma längden av en kurva i $\mathbb{R}^{2}$ i ett intervall $[a, b]$ . Jag kom fram till att sträckan ges av följande uttryck för en funktion $y$ :

$\displaystyle\sqrt{\mathrm{d}y^{2}+\mathrm{d}x^{2}} =\sqrt{1+(\frac{\mathrm{d}y}{\mathrm{d}x})^2}\mathrm{d}x$ .

Denna omskrivning gör att man får ut en differentialoperator ur funktionen, så att funktionen får utseendet som integranden i en integral brukar ha. Då kan man skriva upp integralen:

$\displaystyle d=\int_{a}^{b}\sqrt{1+(\frac{\mathrm{d}y}{\mathrm{d}x})^2}\mathrm{d}x$

Alltså om man integrerar en funktion $f(x)$ behöver man lägga till en faktor $\mathrm{d}x$ efteråt, och man kan då tolka integralen som en area. Men i mitt fall så är ju differentialoperatorn en del av funktionen jag integrerar i sig, så då behöver jag inte lägga till något. Men det får mig att fundera: måste man ha en differentialoperator överhuvudtaget för att kunna integrera? Eller summera ett oändligt antal termer icke-diskret över ett stängt intervall?

Redan vaken, själv tänkte jag gå och lägga mig snart.

Jag borde kunna detta, men blir osäker. Först, vad menar du med differentialoperator i detta sammanhang. Är det dx du kallar diffop? Att man skulle kunna skriva ett integraltecken med gränser och sedan en funktion utan dx efter?

Hemska tanke!

Nu bara spånar jag, take or leave, men när du vill veta volymen av en kropp så skivar du den i tunna skivor, du hittar ett uttryck för skivornas areor A(x) och integrerar A(x) dx; oändligt många infinitesimalt tunna skivor.

När du vill ha en area under f(x) så gör man som du skriver, integrerar ett oändligt antal väldigt smala staplar.

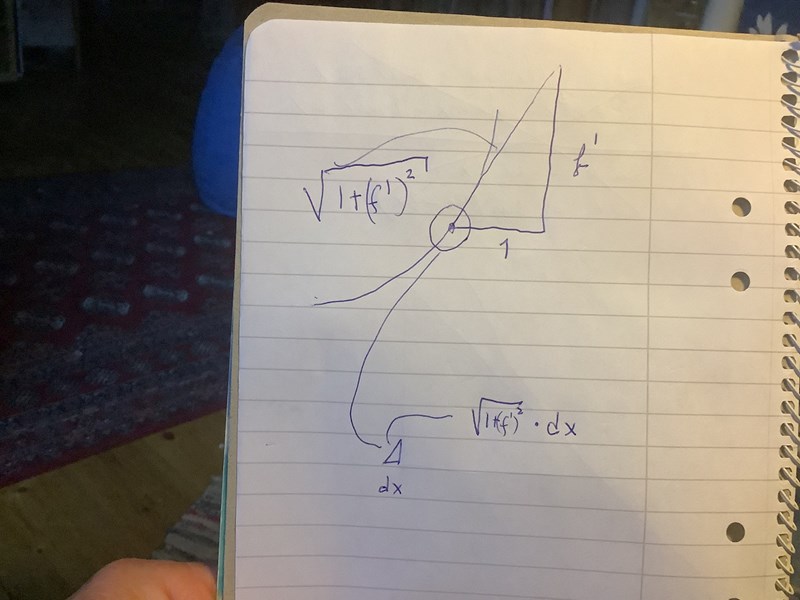
Hur gör vi när vi integrerar fram en kurvlängd? Jag kommer inte ihåg härledningen, men om jag lägger en rätvinklig triangel där kurvan tangerar hypotenusans nedre vänstra hörn (och kateterna är axelparallella) så tänker vi att triangeln har horisontell katet 1. Då är vertikal katet f’ i punkten (jag struntar i + el –, tänker att kurvan går uppåt) och hypotenusan fås ur Pythagoras.

I din integral har du ett rotuttryck; det är längden av hypotenusan i en triangel där horisontella kateten är 1. Men den måste skalas ned till infinitesimal längd. Det gör vi genom att multiplicera med det oändligt korta dx.

Därefter kan vi summera (dvs integrera) de små hypotenusbitarna.

Väldigt informellt skrivet, och jag vet inte om det var det du frågade om. Kanske ljusnade något?

Tack för ditt svar!

Ja, med diffop. menar jag t.ex. $\mathrm{d}x$ . Jag kan ta ett exempel för att illustrera vad som orsakar förvirring hos mig:

"Du vill integrera funktionen $\displaystyle f(x)=x^2+2x-1$ i intervallet $[a, b]$ . Vad blir integralen då?"

Vår funktion ( $f(x)$ ) saknar någon diffop i detta fall. Så när vi integrerar måste vi lägga till en diffop. i slutet:

$\displaystyle \int_{a}^{b}f(x)\mathrm{d}x$

Men i mitt fall har jag något antal längdelement $\mathrm{d}l$ som jag vill summera över ett intervall $[a, b]$ . Dessa längdelement ges av uttrycket jag har ovan, men där har jag ju redan en diffop med i slutet:

$\displaystyle \mathrm{d}l=\sqrt{1+(\frac{\mathrm{d}y}{\mathrm{d}x})^2}\mathrm{d}x$

Så om jag skulle vilja summera dessa längdelement, då behöver jag inte lägga till något $d x$ , men då kan integralen inte heller tolkas som en area på samma sätt som tidigare, eller? Det som orsakar förvirring är att man i det ena fallet aktivt måste lägga till en diffop, medan man i det andra fallet inte behöver det.

Jag förstår inte riktigt vad du menar. Men du triggar igång tankar hos mig, om de nu är synkade med dina:)

Först, jag kallar dx för en differential, inte en differentialoperator. Kolla gärna det.

Sedan, en integral tänker vi ofta som en area. Men jag ser det hellre som en summa; vi summerar oändligt många, oändligt små termer.

Volym: Varje skivas area gånger dess tjocklek dx – summan av många små volymer.

Area: Varje stapels höjd gånger dess bredd dx – summan av många små areor.

Längd: Varje hypotenusas längd – summan av många små längder.

Du har rätt, jag har inte tänkt på det. Kurvlängden är ju en summa av en massa längder, vi multiplicerar inte dx med något mått i en annan dimension, utan lägger bara ihop en följd av små dx, multiplicerade med en dimensionslös skalningsfaktor som ges av derivatan.

Jag vet inte om det ger något men volymen av en cylinder med bottenarea A kan man tänka sig som en integral A dx+ A dx + A dx + …

Arean av en rektangel med höjd h kan man tänka sig som en integral h dx + h dx + …

Och längden av en horisontell sträcka kan man se som integralen dx+dx+dx+…

Om sträckan lutar, säg 60° mot x-axeln är hypotenusan dubbelt så lång som dx, så då blir längden 2dx+2dx+2dx+…

Som sagt, vet inte vad det gav dig men jag lärde mig något.

Svara

Visa senaste svar