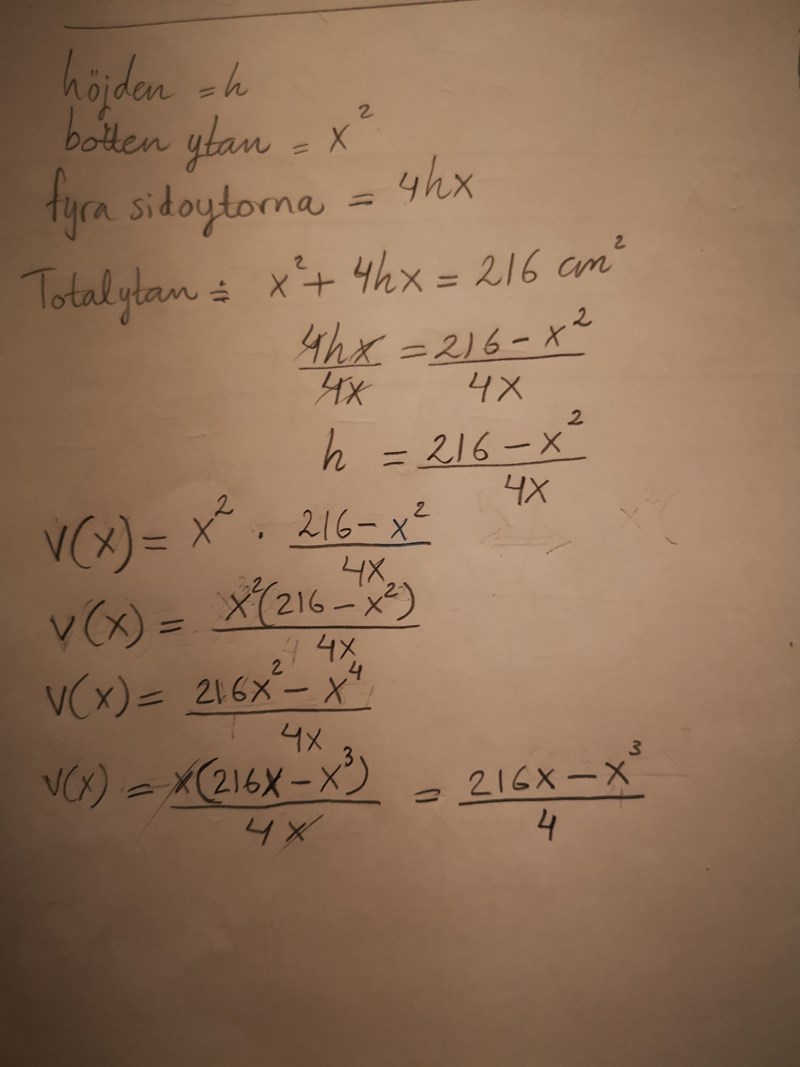Maximal volym
Hej, jag fastnat i den här frågan


Jag löste a) uppgiften, hoppas det är rätt, men fastnat i b) uppgift, jag är inte säker heller om jag har förstått frågan rätt i b). De frågar efter dimensioner när volymen är i maximal läge, alltså längden, brädden och höjden elle hur? Och jag fattar inte heller vad är en maximal volym.. Jag räknade ut volymen i a) uppgiften, men kan volymen vara större? I vilken fall?
Hoppas jag får svar på alla mina funderingar, jag höll på i flera timmar med hjälp av boken och youtube o mellan tråden här men hittar ej bra svar.
Du ska nog fortsätta anta att botten är kvadratisk, men hitta sidan x och höjden h så att sammanlagda ytan är 216, och volymen är maximal, alltså att du inte kan få en större volym.
Detta är den mest standardmässiga uppgiften i Ma3. Det kommer att komma en uppgift av den här typen på varje nationellt prov, det vågar jag lova. Detaljerna skiljer, men strukturen är densamma.
Kalla höjden för h. Det gäller fortfarande att de fyra sidoytorna och bottenarean tillsammans har arean 216 kvadratcentimeter.
Skriv en ekvation som visar att de fyra sidoytorna plus bottenarean har arean 216 kvadratcentimeter. Lös ut h. Då har du fått fram ett samband mellan höjden h och bottenytans sida x. Använd det för att skriva ett uttryck för volymen. Derivera det uttrycket, sätt derivatan lika med 0 och beräkna x.
Laguna skrev:
Du ska nog fortsätta anta att botten är kvadratisk, men hitta sidan x och höjden h så att sammanlagda ytan är 216, och volymen är maximal, alltså att du inte kan få en större volym.
Jag har ju löst ut x värdet, och höjden h har de berättat i frågan att den är 19..
Smaragdalena skrev:Detta är den mest standardmässiga uppgiften i Ma3. Det kommer att komma en uppgift av den här typen på varje nationellt prov, det vågar jag lova. Detaljerna skiljer, men strukturen är densamma.
Kalla höjden för h. Det gäller fortfarande att de fyra sidoytorna och bottenarean tillsammans har arean 216 kvadratcentimeter.
Skriv en ekvation som visar att de fyra sidoytorna plus bottenarean har arean 216 kvadratcentimeter. Lös ut h. Då har du fått fram ett samband mellan höjden h och bottenytans sida x. Använd det för att skriva ett uttryck för volymen. Derivera det uttrycket, sätt derivatan lika med 0 och beräkna x.
Okej, ska lösa det i de steg du nämner.. Men varför bör jag skriva x och h när jag vet värdet på dem? Jag löste ut x:et och h är 19 cm. Va är det som jag behöver göra i b) uppgiften? Jag behöver förstå frågan? Bör jag hitta dimensioner? (höjd, bredd och längd)?
De kunde ha varit tydligare, men det som gäller i både a och b är det som står före a. Det som står i a behöver inte gälla i b.
Laguna skrev:De kunde ha varit tydligare, men det som gäller i både a och b är det som står före a. Det som står i a behöver inte gälla i b.
Aha.. Trodde de hör ihop.. Är mitt svar i a) rätt?
R.i.Al skrev:Laguna skrev:De kunde ha varit tydligare, men det som gäller i både a och b är det som står före a. Det som står i a behöver inte gälla i b.
Aha.. Trodde de hör ihop.. Är mitt svar i a) rätt?
Jag tror det.
Smaragdalena skrev:Detta är den mest standardmässiga uppgiften i Ma3. Det kommer att komma en uppgift av den här typen på varje nationellt prov, det vågar jag lova. Detaljerna skiljer, men strukturen är densamma.
Kalla höjden för h. Det gäller fortfarande att de fyra sidoytorna och bottenarean tillsammans har arean 216 kvadratcentimeter.
Skriv en ekvation som visar att de fyra sidoytorna plus bottenarean har arean 216 kvadratcentimeter. Lös ut h. Då har du fått fram ett samband mellan höjden h och bottenytans sida x. Använd det för att skriva ett uttryck för volymen. Derivera det uttrycket, sätt derivatan lika med 0 och beräkna x.
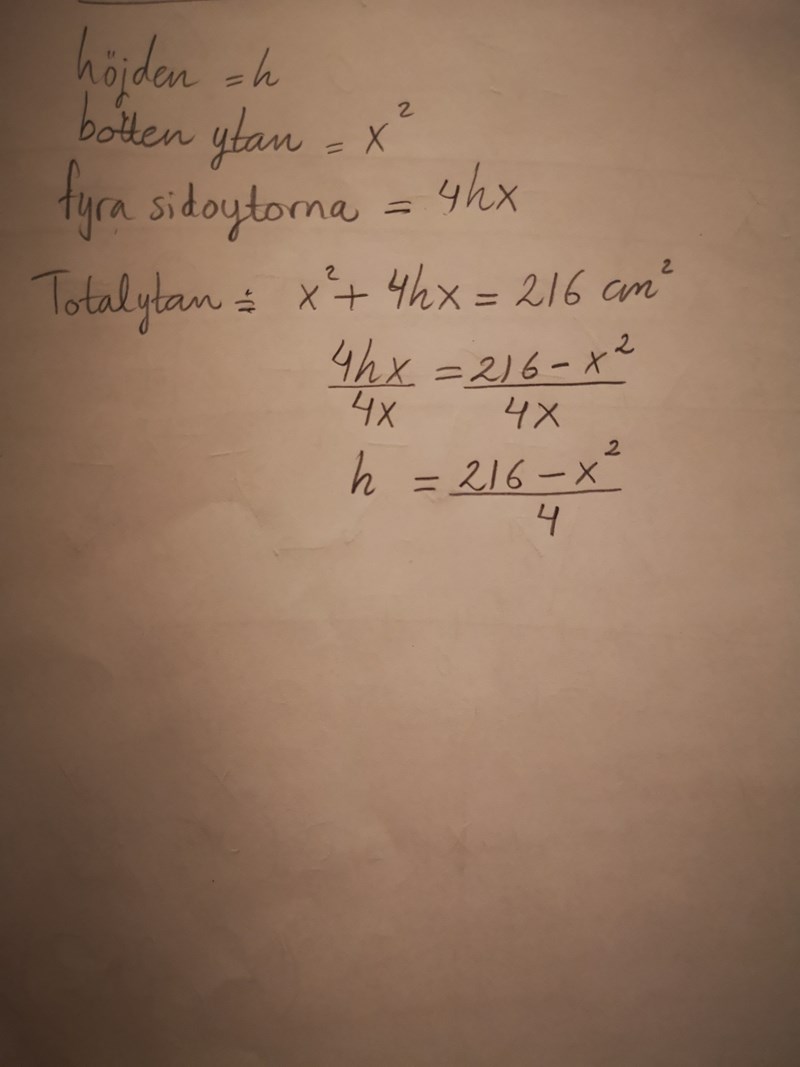 fattar inte hur bör jag göra sen...
fattar inte hur bör jag göra sen...
Du säger att en sådan fråga kan komma på nationella provet, så snälla jag vill förstå va är det jag räknar här, vill inte bara räkna ut det utan förståelse.. Ät det dimensioner, max volym.. Eller? Varför bör jag använda derivatan här?
I a-uppgiften vet du att höjden är 19 cm, i b-uppgiften skall du ta reda på vilket värde på höjden som ger den största volymen. Du kan ha nytta av de beräkningar du gjorde i a-uppgiften när du löser b-uppgiften (men det går att lösa b-uppgiften utan att göra a-uppgiften).
Nu när du har h kan du bilda ett uttryck för volymen.
Fel räknat. Raderat inlägg
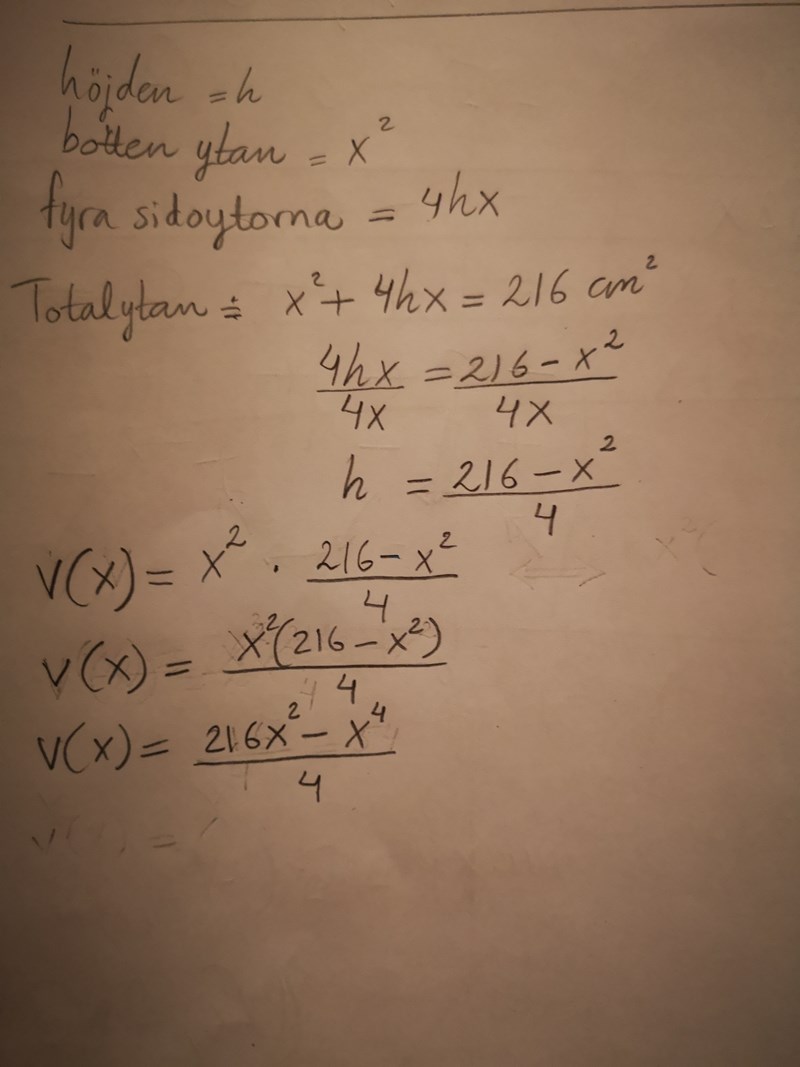 fastnat här igen
fastnat här igen
du glömmer x:et i nämnaren, ska stå 4x.
Smaragdalena skrev:I a-uppgiften vet du att höjden är 19 cm, i b-uppgiften skall du ta reda på vilket värde på höjden som ger den största volymen. Du kan ha nytta av de beräkningar du gjorde i a-uppgiften när du löser b-uppgiften (men det går att lösa b-uppgiften utan att göra a-uppgiften).
Fattar fortfarande ej. Vill de att jag ska ta reda på vilket värde på höjden som ger största volym? Då kan det vara va som helst.. Ju längre höjd desto större volym utan slut... Hehe
Dessutom sa någon att det som stör i a) behöver inte gälla i b)
så du får:
Ja, men rätblocket har en maximal volym som inte kan bli mer än maxvärdet, som ges vid ett visst h.
Alan123 skrev:Ja, men rätblocket har en maximal volym som inte kan bli mer än maxvärdet, som ges vid ett visst h.
När h värdet som är 19 cm är angiven i a) uppgift då ger den den maximal volym som jag kom fram till, 143 cm^3. Va är det då de är ute efter i b) uppgift
Alan123 skrev:
du glömmer x:et i nämnaren, ska stå 4x.
Juste, ursäkta mig jag rättar till..
I upg a) är det givet att du ska bestämma volymen då h är 19 cm. I b) ska du beräkna h, utifrån en maxvolym.
Ja, du får rätt svar.

Edit: Slarvfel... V''(x)=–6x... men resonemanget kvarstår.
Edit 2: cm^3 bör anges i svaret. Huruvida ovanstående är en giltig lösning för NP låter jag andra, mer initierade, bedöma. Det finns säkert ett mindre regelverk hur dessa lösningar skall utformas för att få full poäng.
Trinity skrev:
Edit: Slarvfel... V''(x)=–6x... men resonemanget kvarstår.
Edit 2: cm^3 bör anges i svaret. Huruvida ovanstående är en giltig lösning för NP låter jag andra, mer initierade, bedöma. Det finns säkert ett mindre regelverk hur dessa lösningar skall utformas för att få full poäng.
I fjärde steg där du skrev uttrycket för h värde, du skrev bara x i nämnaren, vart försvann 4
Hej!
Få se om mitt inlägg ökar din förståelse.
- En låda utan lock har en kvadratisk basyta; lådans höjd är centimeter och lådans basyta är kvadratcentimeter.
- Lådans sidoytor är rektanglar vars area är kvadratcentimeter; tillsammans är lådans fem ytor kvadratcentimeter.
- Du vet att den sammanlagda arean är kvadratcentimeter, vilket betyder att och är relaterade via ekvationen
.
Lådans volym () är lika med kubikcentimeter och kan skrivas som en funktion av .
.
- När centimeter är förstås volymen kubikcentimeter.
- När kvadratcentimeter är volymen eftersom då är höjden .
Någonstans mellan dessa värden antar volymen sitt största värde. Frågan är var någonstans?
Om volymen är maximal när så är derivatan . Med hjälp av Produktregeln för derivering beräknas volymfunktionens derivata till funktionen
Du ser att ekvationen är samma sak som ekvationen och den enda positiva lösningen till denna ekvation är
.
Om volymen är maximal någonstans överhuvudtaget så måste den vara det när centimeter.
- Lådans botten () är kvadratcentimeter och lådans höjd () är centimeter.
Albiki skrev:Hej!
Få se om mitt inlägg ökar din förståelse.
- En låda utan lock har en kvadratisk basyta; lådans höjd är centimeter och lådans basyta är kvadratcentimeter.
- Lådans sidoytor är rektanglar vars area är kvadratcentimeter; tillsammans är lådans fem ytor kvadratcentimeter.
- Du vet att den sammanlagda arean är kvadratcentimeter, vilket betyder att och är relaterade via ekvationen
.
Lådans volym () är lika med kubikcentimeter och kan skrivas som en funktion av .
.
- När centimeter är förstås volymen kubikcentimeter.
- När kvadratcentimeter är volymen eftersom då är höjden .
Någonstans mellan dessa värden antar volymen sitt största värde. Frågan är var någonstans?
Hmm ok.. Det ser inte så enkelt ut. Jag löste frågan på mitt sätt, hoppas det är rätt som jag har förstått..
-b.jpg?width=800&upscale=false)
R.i.Al skrev:Albiki skrev:Hej!
Få se om mitt inlägg ökar din förståelse.
- En låda utan lock har en kvadratisk basyta; lådans höjd är centimeter och lådans basyta är kvadratcentimeter.
- Lådans sidoytor är rektanglar vars area är kvadratcentimeter; tillsammans är lådans fem ytor kvadratcentimeter.
- Du vet att den sammanlagda arean är kvadratcentimeter, vilket betyder att och är relaterade via ekvationen
.
Lådans volym () är lika med kubikcentimeter och kan skrivas som en funktion av .
.
- När centimeter är förstås volymen kubikcentimeter.
- När kvadratcentimeter är volymen eftersom då är höjden .
Någonstans mellan dessa värden antar volymen sitt största värde. Frågan är var någonstans?
Hmm ok.. Det ser inte så enkelt ut. Jag löste frågan på mitt sätt, hoppas det är rätt som jag har förstått..
Snyggt!
Du har helt rätt.
Alan123 skrev:R.i.Al skrev:Albiki skrev:Hej!
Få se om mitt inlägg ökar din förståelse.
- En låda utan lock har en kvadratisk basyta; lådans höjd är centimeter och lådans basyta är kvadratcentimeter.
- Lådans sidoytor är rektanglar vars area är kvadratcentimeter; tillsammans är lådans fem ytor kvadratcentimeter.
- Du vet att den sammanlagda arean är kvadratcentimeter, vilket betyder att och är relaterade via ekvationen
.
Lådans volym () är lika med kubikcentimeter och kan skrivas som en funktion av .
.
- När centimeter är förstås volymen kubikcentimeter.
- När kvadratcentimeter är volymen eftersom då är höjden .
Någonstans mellan dessa värden antar volymen sitt största värde. Frågan är var någonstans?
Hmm ok.. Det ser inte så enkelt ut. Jag löste frågan på mitt sätt, hoppas det är rätt som jag har förstått..
Snyggt!
Du har helt rätt.
Äntligen.. Tack :)
R.i.Al skrev:Trinity skrev:
Edit: Slarvfel... V''(x)=–6x... men resonemanget kvarstår.
Edit 2: cm^3 bör anges i svaret. Huruvida ovanstående är en giltig lösning för NP låter jag andra, mer initierade, bedöma. Det finns säkert ett mindre regelverk hur dessa lösningar skall utformas för att få full poäng.
I fjärde steg där du skrev uttrycket för h värde, du skrev bara x i nämnaren, vart försvann 4
Mitt fel! Slarv!
R.i.Al skrev:Albiki skrev:Hej!
Få se om mitt inlägg ökar din förståelse.
- En låda utan lock har en kvadratisk basyta; lådans höjd är centimeter och lådans basyta är kvadratcentimeter.
- Lådans sidoytor är rektanglar vars area är kvadratcentimeter; tillsammans är lådans fem ytor kvadratcentimeter.
- Du vet att den sammanlagda arean är kvadratcentimeter, vilket betyder att och är relaterade via ekvationen
.
Lådans volym () är lika med kubikcentimeter och kan skrivas som en funktion av .
.
- När centimeter är förstås volymen kubikcentimeter.
- När kvadratcentimeter är volymen eftersom då är höjden .
Någonstans mellan dessa värden antar volymen sitt största värde. Frågan är var någonstans?
Hmm ok.. Det ser inte så enkelt ut. Jag löste frågan på mitt sätt, hoppas det är rätt som jag har förstått..
Prydligt. Men hoppa över beräkningar med negativa x. Det tar bara tid. Teckenstudie är bra, men andraderivata snabbare i detta fallet. Hjälper dig att spara tid på prov.
Trinity skrev:R.i.Al skrev:Albiki skrev:Hej!
Få se om mitt inlägg ökar din förståelse.
- En låda utan lock har en kvadratisk basyta; lådans höjd är centimeter och lådans basyta är kvadratcentimeter.
- Lådans sidoytor är rektanglar vars area är kvadratcentimeter; tillsammans är lådans fem ytor kvadratcentimeter.
- Du vet att den sammanlagda arean är kvadratcentimeter, vilket betyder att och är relaterade via ekvationen
.
Lådans volym () är lika med kubikcentimeter och kan skrivas som en funktion av .
.
- När centimeter är förstås volymen kubikcentimeter.
- När kvadratcentimeter är volymen eftersom då är höjden .
Någonstans mellan dessa värden antar volymen sitt största värde. Frågan är var någonstans?
Hmm ok.. Det ser inte så enkelt ut. Jag löste frågan på mitt sätt, hoppas det är rätt som jag har förstått..
Prydligt. Men hoppa över beräkningar med negativa x. Det tar bara tid. Teckenstudie är bra, men andraderivata snabbare i detta fallet. Hjälper dig att spara tid på prov.
Jag räknade negativa x för att få bild på derivatan runt nollställen... Men med andra derivatan får man bara extrempunkterna, inte hur kurvan ser ut runt de kordinater eller hur




.jpg?width=80&crop=0,0,80,80)