Maximering under bivillkor med substitutionsmetoden

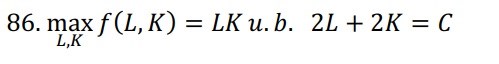
Hoppla hej,

Löser denna uppgift med stor osäkerhet men så här ser påbörjad lösning ut:

substituerar ut L, L= (C-2K)/2

sätter in f(L,K)= LK som då blir $\frac{k (c - 2 k)}{2}$

försöker sedan derivera för att sätta lika med 0

som blir $\frac{k - 4 k}{2}$

Här blir det fel? hur blir deriveringen med kc? eller har jag gjort fel tidigare än så

Hej, jag känner inte till substitutionsmetoden, men om du deriverar $f (k) = \frac{k (c - 2 k)}{2}$ , får du $f' (k) = \frac{c}{2} - 2 k$ .

f är från början tydligen en fkn av två variabler L och K, som jag gissar ska vara reella. Det finns ett samband mellan dem bestämt av 2L+2K=C, där jag förutsätter att C är en konstant. När du substituerar in detta övergår funktionen till att bli en fkn av EN variabel K som dessutom är deriverbar. Eftersom inga randvärden har givits måste ett ev maximum antas i en stationär punkt dvs med derivatan =0. Kontrollera om det ger en maximipunkt på sedvanligt sätt.

Svara