Mekanik 1, Arbete, fjäder (Fysik/Universitet)

Skulle du kunna förklara lite hur du tänker i de olika uppställningarna?

Jag försöker under tiden att försöka sätta mig in i detta och tycker att det hela ser mycket intressant ut.

En vinst för dig kan vara att om du förklarar för mig så är chansen stor att du kommer att se ditt misstag under tiden.

bump

Det är du som har bollen, Johanspeed. ConnyN har svarat på din fråga, du har inte svarat.

Värdelöst forum...

Johanspeed skrev:
Värdelöst forum...

Synd att du känner så. Det finns massor av kunnigt folk här som kan hjälpa till, men det förutsätter att man samarbetar.

Den här uppgiften har verkligen "extra allt".
Friktion och gravitation i lutande plan.
"Fjäderkraft" ifrån i princip en vågrät fjäder som belastas på mitten. Även om det handlar om ett elastiskt band som ser ut att spännas med en yttre kraft.
Vi ska sedan beräkna hastigheten på "partikeln" då den passerar neutralläget.

En av de "tyngre" uppgifterna jag stött på, men om man delar upp den i dess mindre delar så känns den på intet sätt omöjlig att lösa och om jag förstått rätt så har du kommit otroligt långt.
Det skulle vara väldigt intressant om du berättade lite om ditt tänk för oss.

Hoppas att det här kan vara av intresse.

Det här var ett roligt problem!

Jag räknar själv och kommer fram till samma svar som TS. Får ta och räkna om imorgon och se om jag kan se var det blir galet.

Jag tar mig en titt på det du skrev Conny, men jag ser tyvärr lite konstigheter (eller så kanske de inte alls är konstigheter, du har ju fått rätt svar :-)).

Till att börja med tycks du missa att den elastiska kraften inte är konstant; den avtar ju desto längre fram partikeln kommer eftersom förlängningen relativt normalläget blir kortare och kortare ( $\Delta\ell$ minskar, och eftersom $F_e=k\cdot\Delta\ell$ minskar ju då den elastiska kraften $F_e$ ).

En annan sak är att förlängningen av bandet inte är i samma riktning som rörelseriktningen. Den elastiska kraften behöver därför komposantuppdelas.

Och för det tredje verkar du trassla till det vid integralberäkningen genom att låta $x$ vara både konstant och variabel. Kalla istället det ena $x$ :et för $\ell$ så ser du att svaret blir ett annat.

Nu kan det ju så klart vara jag som har fel, och då skulle jag uppskatta om du, Conny, kunde förklara för mig vad jag missförstått gällande ovanstående tre saker.

Tack Alvin. Roligt attvi var två som gillade problemet. Jag ska grunna lite innan jag svarar, men det ser ut att ligga en hel del i det du skriver. Så jag är väldigt tacksam att du engagerar dig.

ConnyN skrev:
Tack Alvin. Roligt att vi var två som gillade problemet. Jag ska grunna lite innan jag svarar, men det ser ut att ligga en hel del i det du skriver. Så jag är väldigt tacksam att du engagerar dig.

Edit: Jag slant med musen och sände svar för tidigt.
Jag har precis läst igenom kapitlet som handlar om just sådana här problem, men behöver träna och lösa uppgifter och den här kom väldigt lämpligt.

Ett tillägg till:

Vi har ett årsmöte i vår vägförening på lördag som jag måste förbereda mig inför, så det blir inget den här veckan tror jag, men min ambition är att gå igenom och rätta upp mina fel och kunna göra en riktig redogörelse för mitt tänk.

Redigerade ditt inlägg så att det som du har skrivit inte hamnar inuti citatmarkeringen - det blir så rörigt och svårläst annars. Du kunde ha redigerat ditt första inlägg, så att du slipper spamma tråden. /Smaragdalena, moderator

AlvinB skrev:
Det här var ett roligt problem!
Jag räknar själv och kommer fram till samma svar som TS. Får ta och räkna om imorgon och se om jag kan se var det blir galet.
Jag tar mig en titt på det du skrev Conny, men jag ser tyvärr lite konstigheter (eller så kanske de inte alls är konstigheter, du har ju fått rätt svar :-)).
Till att börja med tycks du missa att den elastiska kraften inte är konstant; den avtar ju desto längre fram partikeln kommer eftersom förlängningen relativt normalläget blir kortare och kortare ( $\Delta\ell$ minskar, och eftersom $F_e=k\cdot\Delta\ell$ minskar ju då den elastiska kraften $F_e$ ).
En annan sak är att förlängningen av bandet inte är i samma riktning som rörelseriktningen. Den elastiska kraften behöver därför komposantuppdelas.
Och för det tredje verkar du trassla till det vid integralberäkningen genom att låta $x$ vara både konstant och variabel. Kalla istället det ena $x$ :et för $\ell$ så ser du att svaret blir ett annat.
Nu kan det ju så klart vara jag som har fel, och då skulle jag uppskatta om du, Conny, kunde förklara för mig vad jag missförstått gällande ovanstående tre saker.

Rent generellt gäller att den lagrade elstiska energin i en spänd fjäder är

$\frac{1}{2} k (x)^{2}$ där x står för förlängningen och k är fjäderkonstanten.

Man kan få fram det genom att integrera men man kan också resonera sig fram till det; medelkraften är 0,5kx, och totala sträckan är x, således 0,5kx^2

Att energin i detta fall frigörs genom en kraft som inte är parallell med fjäderriktningen borde inte förändra det faktum att hela den inneboende elastiska energin frigörs när det elastiska bandet släpps.

Därför tror jag att ConnyN har rätt (jag har fått samma svar),

den energi som bandet tillför partikeln är

$2 k (2 a^{2} + b^{2} - 2 a \sqrt{a^{2} + b^{2}})$

Nu Alvin ska vi se om jag kan lyckas övertyga dig om att min tankegång är riktig?

Det som har gjort att jag tvivlat en del själv är just komposantuppdelningen, men med egna laborationer i källartaket med uppsatt stretchband både vågrät och lodrät samt samma test med två fjädrar kopplade till varandra så känner jag mig mer övertygad om att jag tänkt rätt.

Hela min uträkning bygger på att kraften som behövs för att sträcka bandet ett visst antal centimeter är lika stor oavsett om jag belastar det lodrät i en ända eller vågrät på mitten.
Vilket jag nu är övertygad om efter de praktiska prov jag gjort.

Om vi tittar på min figur så har jag definierat $l_{1}$ som $x_{1}$ vilket kanske var ett olyckligt val.
Beteckningen $S$ för längden på bandet var också olyckligt då det ofta används för kraften och jag syftade på den totala längden.

Så mer korrekt hade varit $∆ l_{1} = l_{1} - a$ där $l_{1} = \sqrt{a^{2} + b^{2}}$ vilket ger $∆ l = 2 (\sqrt{a^{2} + b^{2}} - a)$

Med det som bakgrund kan man kanske också förstå mina beteckningar vid integreringen?
Gränserna blir då $∆ l$ och 0 och $F (x)$ är $F (∆ l)$ om man nu kan skriva så?

AlvinB skrev:
Till att börja med tycks du missa att den elastiska kraften inte är konstant; den avtar ju desto längre fram partikeln kommer eftersom förlängningen relativt normalläget blir kortare och kortare ( $\Delta\ell$ minskar, och eftersom $F_e=k\cdot\Delta\ell$ minskar ju då den elastiska kraften $F_e$ ).
En annan sak är att förlängningen av bandet inte är i samma riktning som rörelseriktningen. Den elastiska kraften behöver därför komposantuppdelas.

Att kraften inte är konstant hanteras av integralen. Du blandar ihop rörelseriktningen med kraftriktningen på ett sätt jag inte riktigt förstår mig på. Kraften går i bandets riktning och behöver inte komposantuppdelas; resulterande rörelseriktning är irrelevant.

Sedan måste tilläggas att energier inte bryr sig om transienta tillstånd vilket är varför deras hantering ofta är att föredra i komplicerade situationer. Oavsett hur problemet ser ut kan du alltid härleda en elastiskt lagrad potentiell energi till uttrycket:

$U = \frac{k x^{2}}{2}$

Detta är varför egenfrekvensen hos en till synes komplex struktur kan bestämmas genom att modellera denna som en enkel massa och fjäder.

Nu försöker jag kommer tillbaka till detta. Jag förstår att om vi använder att den lagrade potentiella energin är:

$U=\dfrac{k(\Delta\ell)^2}{2}$

faller svaret ut ganska enkelt. Jag ser även att Connys integralberäkning i själva verket är en härledning av denna formel (det rörde till det i min hjärna att både ha $x$ som integrationsgräns och variabel):

$\displaystyle W=\int_0^{\Delta\ell} F\ dx=\int_0^{\Delta\ell}kx\ dx=\frac{k(\Delta\ell)^2}{2}$

Men det jag inte riktigt kan förstå är hur kraften som verkar på partikeln i dess färdriktning kan vara lika stor som kraften i bandets riktning. Kraften går ju som bekant i bandets riktning, men när vi beräknar arbetet som uträttas längs partikelns färdväg integrerar vi ju kraften i färdriktningen. Eftersom den elastiska kraftens riktning är snett uppåt till vänster jämfört med färdriktningen säger min intuition att kraften bör ha två delar; en som pekar uppåt och en som pekar åt vänster.

Jag inser dock den resulterande paradoxen i mitt eget tänkande; när det elastiska bandet spändes upp uträttades ju ett visst arbete som är lika med $k(\Delta\ell)^2/2$ , och denna lagrade energi kan inte försvinna. Det enda rimliga är att hela kraften överförs till partikeln, men detaljerna för hur detta går till begriper jag mig inte riktigt på. Jag tror jag får sätta mig ned med lite snören och häftstift.

Om du drar ner gummibandet precis på mitten, så kommer partikeln att skjutas iväg rakt uppåt. Om du drar ner gummibandet en bit till höger om mittpunkten, kommer partikeln att skjutas snett åt vänster (och likadant spegelvänt).

Tack för återkopplingen Alvin. Denna uppgift har snurrat mycket i mitt huvud i sommar, men nu kan jag börja tro att jag tänkt rätt, men det är tydligt att jag behöver träna mer på mina presentationer.

Fortfarande har jag för mycket gymnasieelev i mig. Det syns när jag rättar mina uppgifter här hemma. Uträkningarna blir ofta rätt, men när jag ser presentationer av lösningarna till facit så ser jag att det finns massor att lära.

AlvinB skrev:
Men det jag inte riktigt kan förstå är hur kraften som verkar på partikeln i dess färdriktning kan vara lika stor som kraften i bandets riktning. Kraften går ju som bekant i bandets riktning, men när vi beräknar arbetet som uträttas längs partikelns färdväg integrerar vi ju kraften i färdriktningen. Eftersom den elastiska kraftens riktning är snett uppåt till vänster jämfört med färdriktningen säger min intuition att kraften bör ha två delar; en som pekar uppåt och en som pekar åt vänster.

Det som verkar ha orsakat frågeställningen är osäkerheter kring vad egentligen integralen Conny ställde upp beräknar. Den beräknar alltså enbart arbetet indirekt eftersom den beräknar den lagrade potentiella energin vilken sedan omsätts till arbete. Det är alltså ursprungskraften man spände bandet med som är i integranden.

Den ursprungliga frågeställaren försökte beräkna arbetet direkt genom att komposantuppdela och bara räkna med de vertikala komponenterna, se nedan för detaljer:

Visa spoiler

Betrakta krafterna som verkar på systemet om vi bortser från friktion och gravitation, se bild nedan:

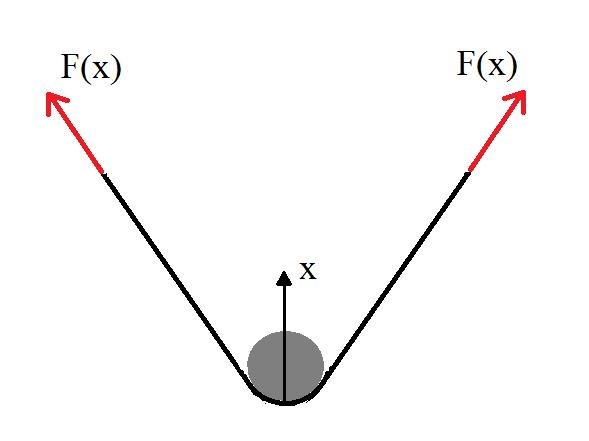
Sättet som TS attackerade problemet på var genom att summera de vertikala komponenterna och sedan beräkna $A r b e t e = K r a f t \times V ä g$ . Vi får krafterna i bandet som:

$F (x) = k (\sqrt{a^{2} + x^{2}} - a)$

där x är avståndet till partikeln. Vi tar fram vertikala resultanten med sinussatsen:

$F_{r e s} (x) = 2 k (\sqrt{a^{2} + x^{2}} - a) \frac{x}{\sqrt{a^{2} + x^{2}}} = 2 k (x - \frac{a x}{\sqrt{a^{2} + x^{2}}})$

Vi får nu det infinitesimala arbetet som:

$d W = F_{r e s} (x) d x$

Vilket sedan ger det totala arbetet över sträckan $b$ :

$W = 2 k \int_{0}^{b} (x - \frac{a x}{\sqrt{a^{2} + x^{2}}}) d x$

Detta är en enkel integral och resultatet är:

$W = 2 k (a^{2} + \frac{b^{2}}{2} - a \sqrt{a^{2} + b^{2}})$

Naturligtvis kan man inte räkna ut arbetet på detta viset eftersom man bara då använder en komponent av kraften som genererats i bandet på grund av den ursprungliga sträckningen från normallängd. Det är lätt att göra detta misstag eftersom man antar att den transversala komponenten inte utför något arbete på partikeln. Man bör betrakta det elastiska bandet och partikeln som ett system på vilken denna kraft verkar. Därmed utför hela kraften ett arbete på systemet eftersom den ämnar att dra ihop bandet till sin ursprungliga form vilket av en händelse driver partikeln framåt. Alltså är det i egenskap av att den genererade kraften drar ihop bandet som bandet sedan utför ett arbete på partikeln.

Jag kan inte hitta något sätt att beräkna arbetet på som inte kräver relativt avancerad beskrivning av hur kraften i bandet faktiskt propagerar genom systemet till partikeln. Att använda lagrad potentiell energi är som vanligt att föredra.

Tack även till Ebola som förklarade så bra hur TS tänkt.

Det skulle vara intressant om nu Johanspeed ville kommentera tråden också.

Inte är väl forumet så värdelöst Johan?

Hej igen!

Vill bara påpeka att jag nu efter ordentliga repetitioner av kapitlen arbete och energi samt några trådar här på pluggakuten har börjat förstå sammanhangen lite bättre.

Jag förstod inte Tures inlägg riktigt fullt ut tidigare, men eftersom vi vill veta den lagrade elastiska energin i bandet så gäller

$U_{e} = \frac{1}{2} k {(x)}^{2}$ och då kan vi också använda enkel geometri som bygger på pythagoras sats för att räkna ut $x$

Nu blev det inte så enkelt ändå att använda pythagoras sats eftersom ekvationerna blev lite långa.
Så det blev enklare med integrering när man kan det. (Jag har en bit dit själv, men ser att beräkningsgången är enklare)

Nu ska jag hoppa vidare till tråden "Var kommer kulan landa" som har tvingat mig att läsa denna tråd igen vid mina praktiska försök att se hur långt kulan kommer.

Så tack en gång till för alla som hjälper till här på pluggakuten.