Mekanik 1 Dynamik - Varför går den inte mot infinity
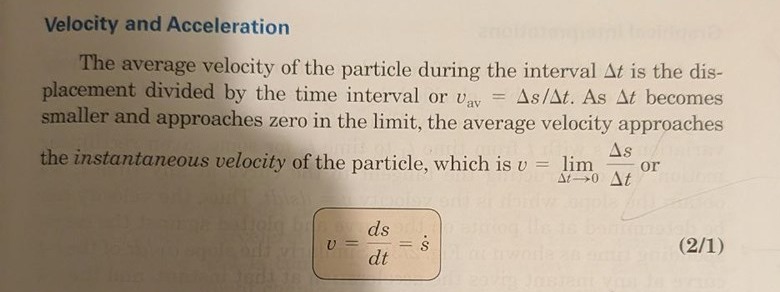
Asså jag tänker att om delta t går mot 0 så blir talet på högerled godtyckligt stort och går mot oändligheten. Dock både delta s och delta är ju smått men fortfarande.
blir ju som du själv noterar mindre och mindre i och med att blir mindre och mindre. Gränsvärdet ovan är ju egentligen bara en fysikalisk variant av "derivata", alltså något på formen
Givet att funktionen är "snäll nog" existerar detta gränsvärde ändligt i alla punkter . Samma sak gäller analogt ditt gränsvärde ovan. Jag tror aldrig att jag har stött på en fysikalisk situation där är kontinuerlig men sådan att den inte är deriverbar med avseende på tid. Någon med mer kunskap kanske kan inflika med några fall där tidsderivatan inte existerar.
naytte skrev:blir ju som du själv noterar mindre och mindre i och med att blir mindre och mindre. Gränsvärdet ovan är ju egentligen bara en fysikalisk variant av "derivata", alltså något på formen
Givet att funktionen är "snäll nog" existerar detta gränsvärde ändligt i alla punkter . Samma sak gäller analogt ditt gränsvärde ovan. Jag tror aldrig att jag har stött på en fysikalisk situation där är kontinuerlig men sådan att den inte är deriverbar med avseende på tid. Någon med mer kunskap kanske kan inflika med några fall där tidsderivatan inte existerar.
Asså jag vet inte, ibland make:ar det sense och ibland inte, även med derivatans definition så känns det mer intuitivt rätt att oavsett vad du har och om vi hade utgått från derivatans definition så skulle alla derivator gå mot infinity även då h går mot 0. Det stämmer ju naturligtvist inte men ändå.
Också när händer det: "där s är kontinuerlig men sådan att den inte är deriverbar med avseende på tid" Är det om det är hål i grafen, det vore ju konstigt i fysikaliska samband då tiden alltid är kontinuerlig tänker jag?
Men täljaren går ju mot noll samtidigt! Då är det väl rimligt att gränsvärdet kan konvergera?
Det jag menar med att jag tror att alltid är deriverbar med avseende på tid är att kontinuitet inte är tillräckligt för deriverbarhet. Det finns patologier som Weierstraß funktion som motbevisar det intuitiva påståendet om att alla kontinuerliga funktioner är deriverbara, men det känns förstås orimligt att en fysikalisk ortsvektor någonsin skulle kunna vara av sådan art…
naytte skrev:Men täljaren går ju mot noll samtidigt! Då är det väl rimligt att gränsvärdet kan konvergera?
Det jag menar med att jag tror att alltid är deriverbar med avseende på tid är att kontinuitet inte är tillräckligt för deriverbarhet. Det finns patologier som Weierstraß funktion som motbevisar det intuitiva påståendet om att alla kontinuerliga funktioner är deriverbara, men det känns förstås orimligt att en fysikalisk ortsvektor någonsin skulle kunna vara av sådan art…
Okej tre saker, ska inte störa dig för mycket, handlar det inte också om hur snabbt de går mot noll?
Andra, vad säger Weierstrass sats om det hela som motsäger det?
Tredje, vad är det som egentligen är kraven för deriverbarhet då?
Edit: chilla ju mindre tidsintervallet är desto mindre sträcka kan punkten färdas på grafen och beroende på hur mycket en punkt hade färdats på grafen, avgör lutningen (vilket är ju är som du sa ty derivatans definition). Asså inte direkt samma men ett sätt att se på det ksk.
Jo, du har rätt i att det spelar roll hur snabbt täljare och nämnare går mot noll.
Weierstraß funktion är en patologi som är kontinuerlig överallt men deriverbar ingenstans, alltså ett motexempel mot att alla kontinuerliga funktioner är deriverbara.
Kravet för deriverbarhet är att derivatan existerar ändligt, alltså att gränsvärdet ovan existerar ändligt. Det finns kanske ekvivalenta karaktäriseringar också som kontinuitet tillsammans med något annat, men jag känner inte till någon sådan.
naytte skrev:Jo, du har rätt i att det spelar roll hur snabbt täljare och nämnare går mot noll.
Weierstraß funktion är en patologi som är kontinuerlig överallt men deriverbar ingenstans, alltså ett motexempel mot att alla kontinuerliga funktioner är deriverbara.
Kravet för deriverbarhet är att derivatan existerar ändligt, alltså att gränsvärdet ovan existerar ändligt.
Lol hur kan en funktion vara kontinuerlig men inte deriverbar, jag tänker mig liksom en kurva eller ett streck men de är deriverbara. Får kolla upp det kanske då.
Påverkar det något om det är ett öppet intervall, alltså om ändpunkterna inte är ifyllda.
Edit: vad är en patologi, jag kollade upp hur funktionen ser ut men ngl är ändå ut som man skulle kunna derivera om man zoomar in, vad är det som gör Weierstrass oderiverbar
För att derivatan i en punkt ska existera måste funktionen vara definierad i en öppen omgivning kring punkten. Om den ska existera på ett intervall får ändpunkterna alltså inte ingå.
En patologi är ett exempel som säger emot vår intuition, i detta fall ett exempel som säger emot vår intuition om att deriverbarhet följer av kontinuitet (vilket alltså inte stämmer!). Det går förstås att bevisa att Weierstraß funktion inte är deriverbar. Finns inte beviset på Wikipedia?
naytte skrev:För att derivatan i en punkt ska existera måste funktionen vara definierad i en öppen omgivning kring punkten. Om den ska existera på ett intervall får ändpunkterna alltså inte ingå.
En patologi är ett exempel som säger emot vår intuition, i detta fall ett exempel som säger emot vår intuition om att deriverbarhet följer av kontinuitet (som alltså inte stämmer!). Det går förstås att bevisa att Weierstraß funktion inte är deriverbar. Finns inte beviset på Wikipedia?
Okej, jo det borde finnas får kolla och så återkommer jag med den infon snart. Men vad händer om punkterna ingår, kan jag fortfarande inte derivera? Liksom varför måste det vara öppen och inte båda. Okej ställer inga mer frågor sen lol
Edit: det utgår från att bevisa att vänster och höger derivata olika, för det finns ju olika derivator, forward, backward och in the middle typ. Det visar sig att de är olika och därför är den inte deriverbar.
Om funktionen i fråga är av typen existerar aldrig , vilket man kan se genom att funktionen t.ex. inte är kontinuerlig i ; man måste ju kunna ”komma från båda hållen i grafen”!
naytte skrev:Om funktionen i fråga är av typen existerar aldrig , vilket man kan se genom att funktionen t.ex. inte är kontinuerlig i ; man måste ju kunna ”komma från båda hållen i grafen”!
mhm du tänker såå, så funktionen är definierad för det öppna värdet a och slutet i b och ger reella värden. Kan man inte tänka samma för om x=a. Om vi då skulle ta f'(a), hur skulle man kunna komma från båda hållen, aa väntaaa, för vi NÅR ALDRIG punkten a så om vi fortsätter zooma in så kommer det alltid finnas någon liten sträcka kvar mellan x=a och x-->a jaha, det är bara svårt att se för det är så litet.
Derivatan existerar inte i heller. Funktionen är ju inte ens definierad där. Det jag menar är att om formen på funktionen är som ovan är funktionen inte deriverbar eftersom det finns åtminstone ett för vilket inte existerar (nämligen ). Men om intervallet vore så kan funktionen mycket väl vara derivarbar, eftersom den högra ändpunkten inte orsakar samma problem längre.
Eller nej, nu talar jag nog i nattmössan! En funktion borde kunna vara derivar på hela sin domän även om ändpunkterna är inkluderade! Om man tar definitionen av derivatan som definitionen ovan borde det definitivt gå...
Det här med att "man måste kunna komma från båda håll" stämmer inte; i definitionen av gränsvärdet kvantifierar vi ju över alla , och om domänen är t.ex. finns det ju inget till höger om , så funktionen kan ju visst vara deriverbar överallt...!
naytte skrev:Eller nej, nu talar jag nog i nattmössan! En funktion borde kunna vara derivar på hela sin domän även om ändpunkterna är inkluderade! Om man tar definitionen av derivatan som definitionen ovan borde det definitivt gå...
Det här med att "man måste kunna komma från båda håll" stämmer inte; i definitionen av gränsvärdet kvantifierar vi ju över alla , och om domänen är t.ex. finns det ju inget till höger om , så funktionen kan ju visst vara deriverbar överallt...!
Så kort sagt, det spelar ingen roll om punkterna är inkluderade eller inte, den kan fortfarande deriverbar i dess valda gränsvärde.
Jo, punkterna måste såklart vara inkluderade om deriverbarhet ska gälla (funktionen måste ju vara definierad i punkten du vill utvärdera derivatan!)
Hmm, håll dig till att derivatan endast kan vara definierad på öppna intervall (a, b) så länge funktionen är definierad på minst [a, b]. Det strider inte mot de definitioner som används på F. De flesta av våra föreläsare tycker "vänster- och högerderivator" är nonsens.
Jag håller med om att det är nonsens men om funktionen är definierad på t.ex. , varför skulle derivatan inte kunna existera i ändpunkterna? Gränsvärdet borde definitivt kunna existera, eller?
Derivatan är definierad som ett gränsvärde och ett gränsvärde definieras som att man närma sig från alla håll. Men jag läste lite om det. Om man justerar sin definition för derivatan (på något sätt) kan man tydligen komma runt detta. Men att man ska ha öppna mängder och eller ha inre punkter förekommer även i alla bevis i flervarren och komplexen där derivering används.
Jag håller med om din första mening men i vissa fall kan det ju lika gärna bara finnas ett håll. Detta är definitionen jag tänker på:
Det viktiga i det här sammanhanget är kvantifieringen över . Eftersom vi bara kvantifierar över de i domänen till , och det ju inte finns något till höger om om domänen är t.ex. , så behöver vi i gränsvärdets definition väl endast "komma från ett håll" i det fallet?
Tillägg: 21 jan 2026 08:29
Men jag har också endast sett differentiering på öppna intervall, därav min tidigare kommentar om att man behöver öppna omgivningar. Men jag tror inte att det stämmer, även om det ofta används i bevis. En funktion kan ju vara differentierbar på även om man endast kräver differentierbarhet på ; det föregående kravet är ju starkare om det är möjligt.
Jag vet inte riktigt hur man hanterar utanför definitionsmängden. Att det ska komma från båda håll beror ju på att det är absolutbelopp. Men du har ju en poäng i att det är konstigt att som inte ens tillhör definitionsmängden, och således inte "testas" i , kan användas för att upphöra kravet.
Jag tror inte att man måste hantera de utanför domänen alls; de existerar inte såvitt funktionen vet.
Sett till definitionen tror jag inte att det stämmer att en funktion inte kan vara deriverbar på . Bevisen använder ju ofta kontinuitet på och deriverbarhet på , men det betyder ju inte att funktionen inte kan vara deriverbar på , bara att det tydligen är en starkare hypotes än vad som krävs.
Om man oroar sig över att man inte kan ”komma från båda håll” gällande deriverbarhet på borde man väl ha samma invändningar gällande kontinuitet på ? Definitionerna är ju nästan identiska.
Tillägg: 21 jan 2026 15:44
Vi kan skapa en ny tråd om detta. Det är en intressant diskussion men vi har svävat bort en del från ursprungsämnet nu.



