Mekanik - Kan man få riktningarna att bli "rätt" automatiskt?

Derivera $\mathbf{L}$ alltså $\displaystyle I_A \cdot -\dot{{\alpha}} \hat{z}$, och sätt lika med $\mathbf{M}$. 

Momentet och förändringen av rmm är alltid samma så man kan använda den ena för att ta reda på riktning av den andra. 

Var kommer minustecknet ifrån? Jag tänker att vinkelhastigheten har negativt tecken i sig redan eftersom vinkeln blir mindre. Går det inte att tänka så?

Nu vet jag inte hur du satt ditt x och y men jag antar "som vanligt". Och då ser vi enligt bland annat skruvregeln att rotationsvektorn är riktad in i pappret. 

Tecknet ingår inte på det sättet i beteckningen för de olika storheterna. Man behöver tecknet för att göra beräkningar. 

Jag håller med om att rotationsvektorn ska peka inåt. Men om jag bestämmer att vinkeln $\alpha$ definieras som i bilden ovan, och vi vet att $\alpha$ har ett tidsberoende, då borde väl $\dot{\alpha} < 0$ av sig självt? Eftersom vinkeln minskar då tyngdkraften får skivan att rotera.

 Ja, asså vi kan förvänta oss det ja. Men för att våra beräkningar ska bli korrekt behöver vi lägga till tecken. Det kan finnas tecken som inte är lika uppenbara så att hålla koll på både tydliga och otydliga tecken är inte en bra ide. 

Inser nu att det kanske har blivit lite konstigt med mina beteckningar. Vinkeln $\alpha$ är väl konstant haha?

Om du definierat den mellan r och den långa sidan så ja, annars, vilket jag trodde, alltså mellan r och x-axeln, så nej. 

Det är viktigt att rita ut koordinataxlarna i sin figur, men det har du förmodligen gjort på ditt papper.

Jo precis, jag tänkte mig en vinkel mellan $x$-axeln och ortsvektorn till masscentrum. Tydligen lyckades jag bli förvirrad av min egen figur och feltolka den...

Nu är det dags att slagga, med andra ord!

Återkommer imorgon.

Älskar när det händer! :)

Okej, nu tror jag att jag fick till det.

Vi har $\mathbf{L}_A = -I_A \dot{\alpha}\cdot \hat{z}$, eftersom högerhandsregeln ger en vektor som pekar i negativ $z$-riktning.

Vidare har vi $\mathbf{M}_A = \mathbf{r}\times -mg\hat{y} = -mgr\sin\varphi \cdot\hat{z}$, där $\varphi$ betecknar vinkeln mellan vektorerna. Vi får alltså även här en vektor som pekar i negativ $z$-riktning.

Newtons andra lag ger:

$\displaystyle -I_A \ddot{\alpha}\hat{z}=-mgr\sin\varphi \cdot\hat{z}$

Vi kan stryka enhetsvektorerna och minustecknen och blir kvar med:

$\displaystyle I_A \ddot{\alpha} = mgr\sin\varphi$

Och resten är enkel!

Ser det bra ut så?

Tillägg: 21 maj 2025 13:21

Varför blir formatteringen så konstig om man försöker använda \ddot ? Det ser ju bra ut med bara \dot...

Snyggt! 

Latexen här är väl inte jättesmooth. Finns det något som \displaystyle som fungerar för annat (vektorer, hattar, bars osv). De blir ofta fula för mig.

Visst spelar det ingen roll mellan vilken vektor och $x$-axeln vi väljer att mäta $\alpha$? Jag valde ju den vinkeln ganska godtyckligt.

Det finns nästan inget som spelar roll om man tar hänsyn till det i alla sina beräkningar. 

Men om jag hade dragit min figur så här:

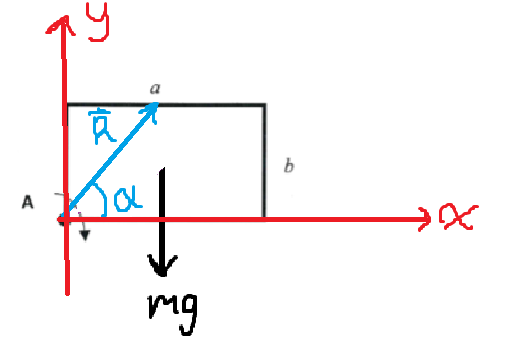
Hade något förändrats då för uttrycket för skivans rörelsemängdsmoment?

Eller tänker vi att skivan är en "punktmassa" med tröghetsmoment $I_A$ och massa $m$, dvs vinkeln $\alpha$ i uttrycket $I\dot{\alpha}$ är punktmassans (masscentrets) vinkel runt rotationsaxeln?

Vinkelhastigheten är samma för alla punkter på objektet så det spelar ingen roll var du sätter den. För att beräkna $\vec{L}$ givet ett tröghetsmoment och och vinkelhastighet är det enda kravet att rotationen och tröghetsmomentet är definierade runt samma punkt/axel.  

Yes precis, det var det jag tänkte! Ville bara bekräfta att min kassa fysikaliska intution stämde för en gångs skull.

Tröghetsmomentet ihop med vinkelhastigheten sköter allt för dig, vilket är skönt. Skulle man vilja räkna med definitionen $\vec{r} \times m\vec{v}$ måste man hela tiden beräkna enskilda $\vec{L}_i$ med $\vec{v}$ för små massdelar med $\vec{v}=\vec{\omega} \times \vec{r}$ och sedan summera allt ihop. Det fiffiga är all summation av massdelar redan är gjord i vår definition av $I$. Väldigt fiffigt. Det är ju såklart ett sådan resonemang som sker i härledningen av formeln. 

Precis, problemet i vårt fall är att $\mathbf{v}$ blir annorlunda beroende på vilket masselement vi betraktar eftersom vi rör oss i en cirkel? Men om vi hade haft translationell rörelse istället hade det varit helt OK trots att vi inte jobbar med en punktmassa, eller hur? Eftersom alla masselement har samma hastighet.

Alltså i en situation som denna där en kloss bara rör sig rakt ned:

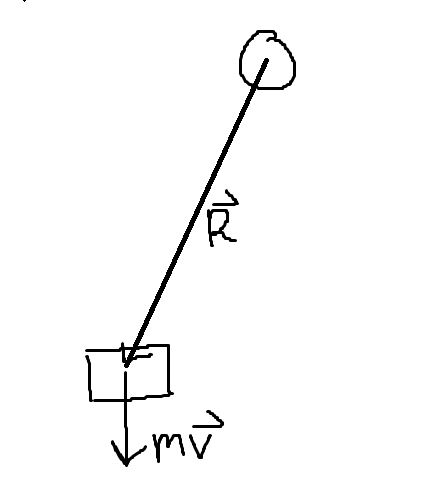
Så hade vi utan förbehåll kunnat räkna ut $\mathbf{L}_O$ genom $\mathbf{R}\times m\mathbf{v}$ eftersom klossen rör sig translationellt.

Så borde det vara ja.