Minsta sammanlagda arean, vinkel x
Hej! Jag har fastnat på följande uppgift:
Jag provade ansätta cirkeln som g(x) och linjen som f(x) och skriva likhet därmellan. Absolutbeloppet från origo till cirklen är 1, vilket gör det möjligt att skriva (och lösa) följande likhet:
sin²x+cos²x=1-x²
Här kommer jag inte vidare

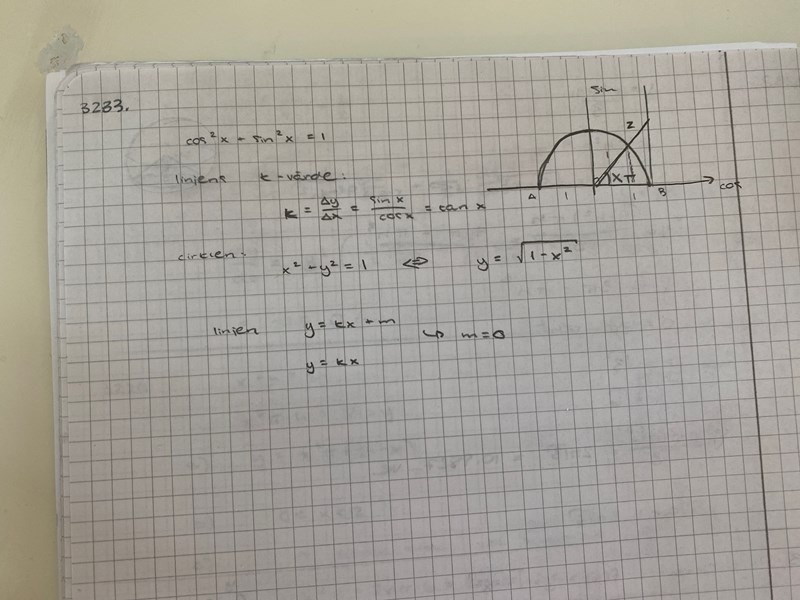
Jag skulle först bestämma def.området för x - mellan vilka vinklar kan x ligga? x räknas i radianer
Sedan skulle jag uttrycka den vertikala höjden i den rätvinkliga triangeln, h, i x med hjälp av tan x
Slutligen hitta ett uttryck för arean av den rätvinkliga triangeln i enbart x
För att därefter den streckade arean ovanför cirkelbågen som differensen av triangelarean och cirkelsektorns area.
Detta uttryck tillsammans arean av cirkelsektorn till vänster blir den sökta arean - som funktion av x
Derivera funktionen och sök extremvärdet (förhoppningsvis ett min)
Henning skrev:Jag skulle först bestämma def.området för x - mellan vilka vinklar kan x ligga? x räknas i radianer
Sedan skulle jag uttrycka den vertikala höjden i den rätvinkliga triangeln, h, i x med hjälp av tan x
Slutligen hitta ett uttryck för arean av den rätvinkliga triangeln i enbart x
För att därefter den streckade arean ovanför cirkelbågen som differensen av triangelarean och cirkelsektorns area.Detta uttryck tillsammans arean av cirkelsektorn till vänster blir den sökta arean - som funktion av x
Derivera funktionen och sök extremvärdet (förhoppningsvis ett min)
Om vi först beräknar arean av den rätvinkliga triangeln får vi -
Men tan x=h/1 dvs h=tan x , vilket innebär att
Arean av den ofyllda cirkelsektorn blir -
På motsvarande sätt blir arean för den fyllda cirkelsektorn till vänster -
Nu kan du bilda uttrycket för den sökta arean T(x) med hjälp av uttrycken ovan
Vi får nu den sökta arean uttryckt i x som
Nu om inte förr bör vi ta fram def.området, dvs tillåtna värden (vinklar) för x. Vilket blir:
Intressant är att undersöka vilket värde T närmar sig då x närmar sig 90 grader . .........
Då vi deriverar T(x) får vi:
Vilka nollställen ger derivatan ?
Derivatans nollställen fås nu ur ekvationen
Denna ekvation har oändligt många lösningar, men tack vare insikten om def.området återstår endast
Återstår att utröna om detta är ett min, vilket kan göras på flera sätt.
T ex genom att undersöka gränsvärdet för T då x går mot 90 grader.
Eller att göra en teckentabell för derivatan runt värdet 45 grader, t ex se på tecknet för derivatan för 30 resp 60 grader (vilka har exakta värden för cos för dessa värden)
Vi finner att extremvärdet står för ett min och slutligen kan vi beräkna arean för denna vinkel, dvs


