Mönster och formler
Hejsan!
Jag har svårt för att hitta en formel till ett mönster när det inte ökar med lika många hela tiden. Om t.ex. figur 1 har 5 stickor, figur 2 har 7 stickor och figur 3 har 9 stickor så vet jag att det ökar med 2 hela tiden och då kan jag hitta en formel med hjälp av detta. Men om det inte ökar med lika många hela tiden så vet jag inte hur man hittar en formel, ibland lyckas jag se det och ibland inte. Skulle någon kunna hjälpa mig med detta? Det kanske är svårt att tolka vad jag menar men jag vet inte hur jag ska förklara på ett bättre sätt.
Tack på förhand!
Ett knep som funkar ibland är att skriva ut hur mycket differenserna ändras för varje steg.
EDIT: La till ett borttappat ord - hoppas det är mer begripligt nu!
Smaragdalena skrev:Ett knep som funkar ibland är att skriva ut hur mycket differenserna för varje steg.
Ja precis, och om ökningen är konstant så är det lätt att hitta formeln, men om den inte är konstant så vet jag inte hur man ska tänka. Har du något knep eller sätt som man kan använda i såna fall? Tack för att du svarar!
Om det är en figur så kan man ju också titta på hur figuren utvecklas och om det är något man känner igen från varje figur. Om du har en figur som består av punkter typ detta exempel . (Skit i att mina ringar är lite olika stora :P)
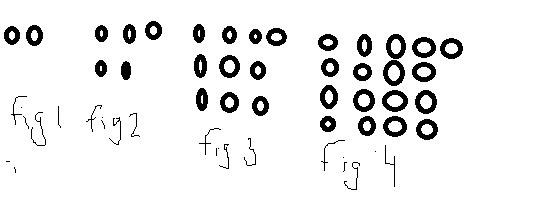
Här kan man se att varje figur ser ut som en kvadrat av ringar med en extra ring
ex. figur 1 en kvadrat som är 1x1 ringar + en extra längst ut
figur 2 en kvadrat som är 2x2 ringar + en extra längst ut
figur 3 är en kvadrat som är 3x3 ringar+ en extra längst ut
figur 4 är en kvadrat som är 4x4 ringar + en extra längst ut.
Den n:te figuren borde då ha ringar
till exempel 2---5---10---17---26---37
differenserna är 3---5---7---9---11
differensen mellan differenserna är 2---2---2---2
Då kan du hitta en formel som gäller för andra raden, och sedan kan du använda den formeln för att få fram en formel för den första raden. Pröva själv på min uppgift! Kör du fast, så fråga igen.
Smaragdalena skrev:till exempel 2---5---10---17---26---37
differenserna är 3---5---7---9---11
differensen mellan differenserna är 2---2---2---2
Då kan du hitta en formel som gäller för andra raden, och sedan kan du använda den formeln för att få fram en formel för den första raden. Pröva själv på min uppgift! Kör du fast, så fråga igen.
Jag kom fram till att differenserna 3, 5, 7, 9 och 11 får man fram genom 2n+1. Så nu ska jag använda den här formeln för att hitta den "riktiga formeln" men jag vet inte hur :(
Jämför med bilderna Jonto har postat - han råkade välja precis samma tal som jag (och det visste jag inte om när jag skrev mitt inlägg).
Smaragdalena skrev:Jämför med bilderna Jonto har postat - han råkade välja precis samma tal som jag (och det visste jag inte om när jag skrev mitt inlägg).
Mm hans sätt förstod jag, men jag kan inte koppla det till ditt sätt. Vad ska jag göra med formeln 2n+1 för att få fram n^2+1 ? jag har försökt men jag kommer inte fram till något
Om differenserna blir konstanta efter två omgångar av differenser, är det en andragradsfunktion man har att göra med.
Smaragdalena skrev:Om differenserna blir konstanta efter två omgångar av differenser, är det en andragradsfunktion man har att göra med.
Okej. Vi har inte lärt oss andragradsfunktioner än. Så jag antar att jag inte kan använda mig av det här sättet, men använder du dig av något annat sätt för att hitta en formel?
Ursäkta mig om jag frågar för mycket men jag tycker att det är så krångligt att hitta en formel när ökningen inte är konstant.
Ja, det är t.ex. krångligt att hitta en formel för hur många ringar det är i figur 42, i Jontos serie ovan.
Men det är betydligt lättare att hitta en formel för hur många ringar FLER det är i figur 42, jämfört med figur 41.
Eller, som man ofta skriver, hur många fler ringar det är i figur N jämfört med figur (N-1).
Figur 2 har 3 ringar fler än figur 1
Figur 3 har 5 ringar fler än figur 2
Figur 4 har 7 ringar fler än figur 3
Figur N har (2N-1) ringar fler än figur (N-1)
Om ni inte har lärt er andragradsfunktioner borde det inte hända att differenserna ökar. Hur ska ni uttrycka formeln?
Har du ett exempel på när differenserna inte är lika?





