Multiplikation och division med komplexa tal
3) Man har de komplexa talen
u=2(cos (-5π/4) +i sin (-5π/4) ,
z=6(cos (5π/3) +i sin (5π/3)
och w= 4(cos (pi/3) +i sin (pi/3) .
a) Bestäm talet
uz/w²
på polär form, där argumentet ges i intervallet 0 ≤arg uz/w² ≤ 2π.
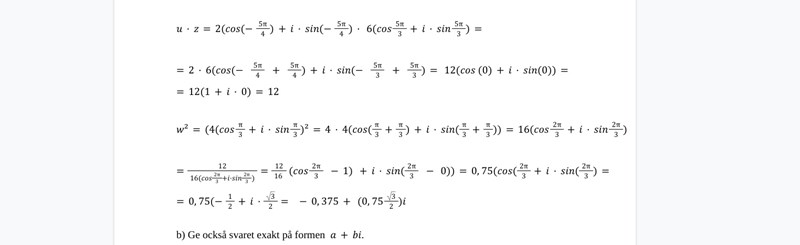 Såhär har jag försökt lösa den, är det rätt?
Såhär har jag försökt lösa den, är det rätt?
oops du hade gjort som jag skrev...
ehm, då måste den vara korrekt?
Förhoppningsvis, jag har inte lusläst din lösning, bara tittat på den metod du använder, och den är rätt!
hmm, då kanske den är fel ändå, har du lust att lusläsa den?
du gör fel på andra raden argumentet har fel nämnare på andra termen i cos och sin uttrycken. Står -5pi/4+5pi/4 ska vara -5pi/4+5pi/3
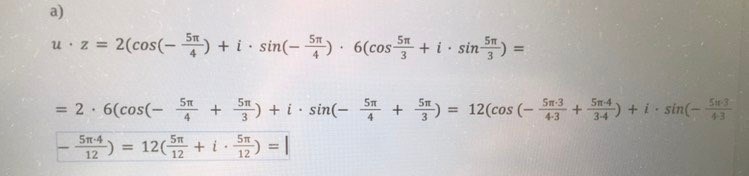 oj, ja såg det nu. Är detta rätt? Vet bara inte hur jag ska göra sista ledet..
oj, ja såg det nu. Är detta rätt? Vet bara inte hur jag ska göra sista ledet..
så långt OK.
Nu ska du dela med w2 som du gjorde i första inlägget
 Nu gjorde jag såhär, man kanske kan hitta en mindre gemensam nämnare? Jag valde 24..
Nu gjorde jag såhär, man kanske kan hitta en mindre gemensam nämnare? Jag valde 24..
Ja, du kan förenkla 6/24 till ett enklare bråk.
är det jag gjort rätt, för får ändå ett bra tal i slutet (pi/4). Hur kan jag göra annars?
Dina uträkningar är rätt, men läs uppgiften igen så att du svarar på rätt form.
Ska vara i detta tror jag..
Men argumentet blir mindre än 0?
OliviaH skrev:Ska vara i detta tror jag..
Rätt, förutom att det saknas en högerparentes.
Men argumentet blir mindre än 0?
Ja, men du vet att cosinus- och sinusfunktionerna har en periodicitet på 2pi, så du kan lägga till 2pi till argumentet och ändå få samma komplexa tal.
ja, det har 2 pi som period, och om jag lägger till 2 pi så får jag positiv pi/4 ellerhur? Hur skriver jag det i beräkningen?
Nej, hur räknade du nu?
Rita in talet i det komplexa talplanet, så slipper du nog den sortens fel.
vet inte hur jag ritar in det
-pi/4+2pi är inte lika med pi/4, lika lite som -0,25+2 är lika med 0,25.
jag förstod det nu, men vet inte hur jag ska göra
Menar du att du inte vet hur du ska beräkna ?
OliviaH skrev:vet inte hur jag ritar in det
Som i ett vanligt koordinatsystem, med realdelen på x-axeln och imaginärdelen på y-axeln.
ja, men då är det i nu har jag pi? Hur gör jag då
OliviaH skrev:ja, men då är det i nu har jag pi? Hur gör jag då
Pi är ett vanligt reellt tal som hanteras på exakt samma sätt som andra reella tal.
Vet du då hur du ska kunna förenkla ?
Ursäkta, men jag vet inte ..
Hur mycket är ?
OliviaH skrev:
Ursäkta, men jag vet inte ..
Det här är enklare än du tror.
Talet pi är en gemensam faktor för de båda termerna, så du kan bryta ut det talet och då få .
Nu behöver du bara förenkla och sedan multiplicera pi med det resultatet.
Om du helt har glömt bort detta så kan vi påminna om addition och subtration av bråk.
Ja, och därför är .
Kommer du vidare då?
ja, då förstår jag. har jag då. Kan jag svara så? Ska svara i a+bi. Min nästa fråga blir ju då hur jag vet vad 7pi/4 har för värde...
Läs frågan igen. Vad står det där om hur du ska svara?
på a) kan jag svara som ovan antar jag, men på b ska jag svara a+bi, då vet jag inte hur jag ska göra
Att på a-frågan svara att är lika med är rätt.
Men vad menar du med "på b"? Hur lyder den frågan?
kanske inte skrivit den här, men b) uppgiften är "ge också svaret exakt på formen a+bi".
OK, då behöver du bestämma det exakta värdet av och .
om jag tittar i en enhetscirkel så ser man att sin har ett värde på
Ja det stämmer. Då kan du besvara b-uppgiften.
får 0,75-0,75i?
Nej det stämmer inte. Multiplicera in 0,75 (dvs 3/4) i parentesen och skriv om på så enkel form som möjligt.
 såhär?
såhär?
Nej det stämmer inte heller.
Repetera det här avsnittet om hur man multiplicerar ett tal med ett uttryck inom parenteser, dvs den distributiva lagen.
Du måste alltså multiplicera båda termerna inom parenteserna med 0,75.
Och det stämmer inte heller att är lika med . Hur resonerade du där?
menar du cos och sinparentesen? Resonerade fel, resonerade att det var roten ur 2 ^ med 3
Ja, men är ju inte lika med utan istället , vilket är lika med .
ja, fel av mig
OK, men får du till multplikationen med 0,75 nu?
Menar du ?
ja
Då är det rätt.
är det slutsvaret?
Ja, det är svaret på fråga b.




