Navier-Stokes - vad hände med de andra kompontenterna i gradienten av trycket?

Hej!

Jag har just läst härledningen till Navier-Stokes ekvation för inkompressibla flöden,

$\displaystyle \rho \frac{D\mathbf{v}}{Dt}=\rho \mathbf{g}-\nabla P+\mu \nabla^2\mathbf{v}$

För att bekanta mig med ekvationen studerar jag just nu ett exempel ur min kursbok, som framgår nedan:

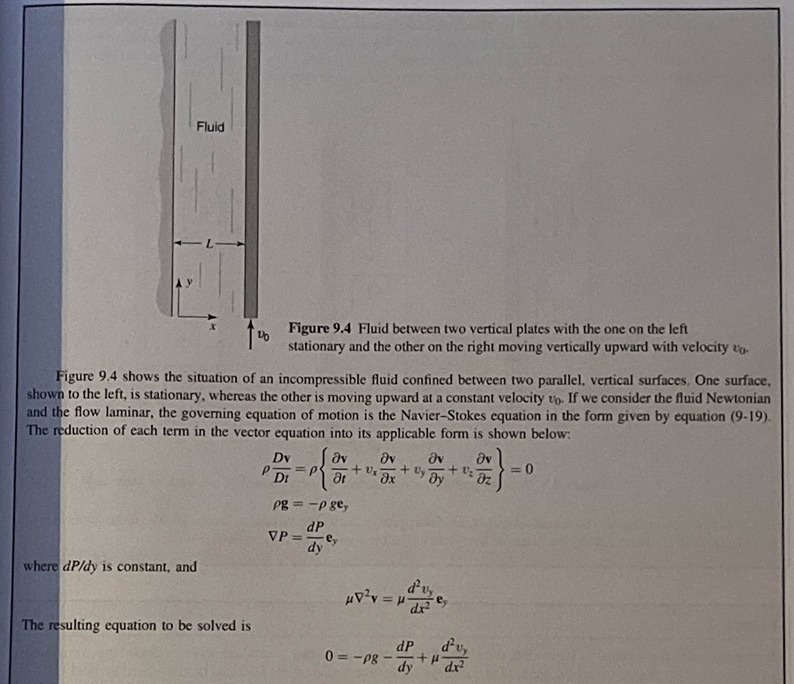
Så som koordinatsystemet är lagt har ju gravitationen bara en komponent, så jag är med på varför $\rho \mathbf{g}=-\rho g\mathbf{e}_y$ . Men vad är det som händer med tryckgradienten? Tryckgradienten kan väl mycket väl ha nollskilda komponenter i $x$ - och $z$ -riktningen?

Om du tar med x- och z-komponenterna av ekvationen så får du att $\frac{\partial P}{\partial z} = \frac{\partial P}{\partial x} = 0$ . Så P beror endast på y.

Okej, jag tror att jag är med, men för att vara säker så försöker jag visa det explicit nedan. Ekvationen i endast $x$ -riktningen blir då t.ex. (om vi sätter alla konstanter till $1$ )

$\displaystyle \frac{Dv_x}{Dt}=g_x-\frac{\partial P}{\partial x}+\nabla^2v_x$

$\nabla^2v_x=0$ eftersom hastigheten inte har någon komponent i $x$ -led, $g_x= 0$ av samma anledning och $\frac{Dv_x}{Dt}=0$ likaså. Då ser man att $\partial_x P = 0$ ?

Ja. Precis.

En fråga till, om du har tid. Hur vet man att $D\mathbf{v}/Dt = 0$ (översta uttrycket i bilden)? Jag förstår inte hur författarna kommer fram till det.

Man har nog gjort ansatsen $\vec{v} = v_{y} (x) {\vec{e}}_{y}$ . Då blir $\frac{D \vec{v}}{D t} = 0$ .

Jag hänger ändå inte riktigt med. Låt säga att vi har ansatsen du skrev. Då har vi

$\displaystyle \frac{D\mathbf{v}}{Dt}=\frac{\partial \mathbf{v}}{\partial t}+v_x\frac{\partial \mathbf{v}}{\partial x}+v_y \frac{\partial \mathbf{v}}{\partial y}+v_z \frac{\partial \mathbf{v}}{\partial z}=\dot{\mathbf{v}}+v_y\frac{\partial v_y}{\partial x}\mathbf{e}_y$

Varför blir detta noll?

Stationär strömning. Inget explicit tidsberoende.

v_x = v_z = 0.

Kvar blir v_y(dv_y/dy)e_y = 0. v_y beror bara på x enligt ansats.

Ah, jag skrev upp det fel...!

Hur vet vi att flödet är stationärt?

Det blir det med den ansatsen som vi gjorde, eftersom t inte finns med explicit i vår ansats.

Okej, då är jag med!

Men hur vet man om man får göra en sådan ansats eller ej? Det är ju läskigt att skriva en tentamen i en kurs där man får hitta på saker själv haha

Ja. Se denna https://www.pluggakuten.se/trad/berakna-hastighetsfaltet-u/.

Svara

Visa senaste svar