Nollställen

De ända förkunskaper jag har ang nollställen är att en funktion av grad n har n-1 stycken nollställen

Här har du fått något om bakfoten. En funktion av grad n har maximalt n nollställen, och maximalt n - 1 extrempunkter. 

Prova att bryta ut den största gemensamma faktorn ur funktionen. Vad får du för funktionsuttryck? :)

Ett polynom av grad n har n nollställen, annars var det rätt.

Kan du faktorisera uttrycket?

Eller ett annat angreppssätt: kan du se några nollställen till uttrycket?

Detta får jag när jag när jag faktoriserar funktionen, men jag förstår fortfarande inte hur detta kan hjälpa mig? Svaret enligt facit är 2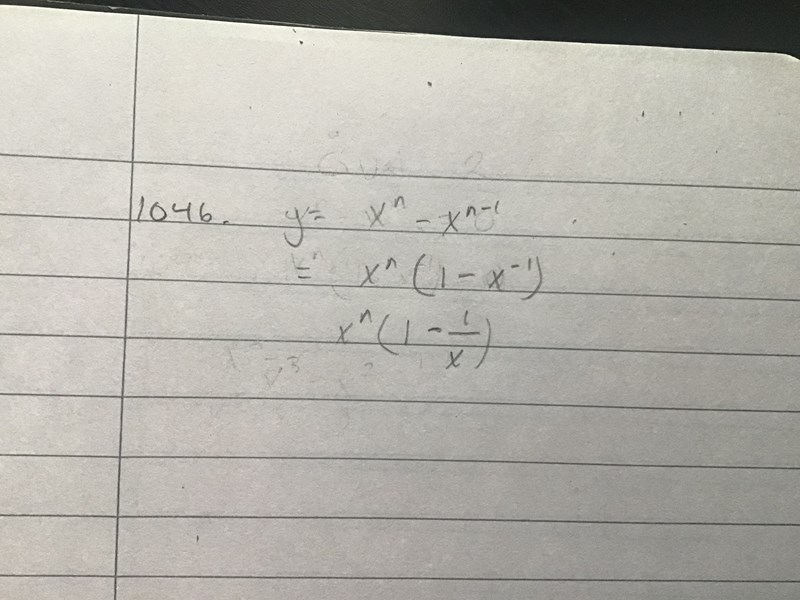

Bryt ut lite mindre, så att det i parentesen är ett polynom. Då kan du använda nollproduktmetoden för att hitta nollställena.

Är detta rätt?

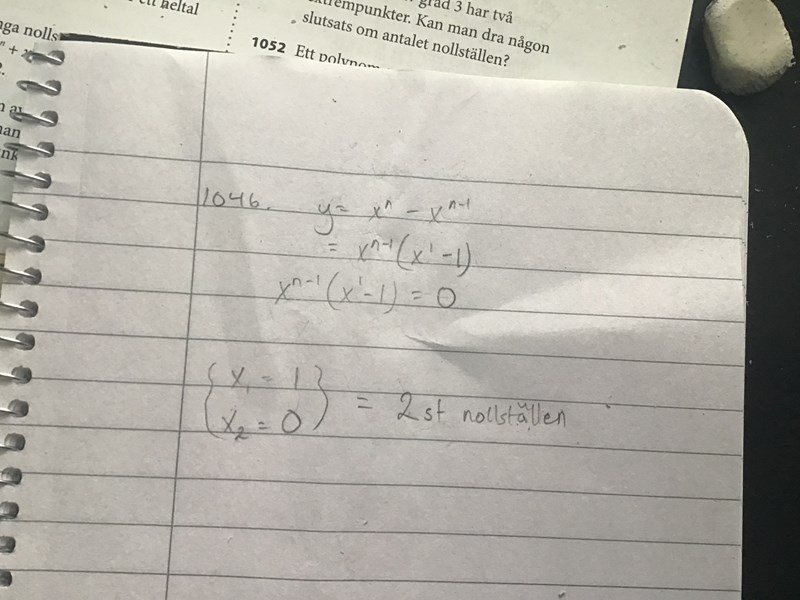
Men jag fattar inte varför det var så viktigt att nämna att n är ett heltal större än 1?

Om n kunde vara mindre än ett, skulle funktionen kunna vara $y=x^1-x^0=x-1$, som har ett nollställe, exempelvis. 

Enligt algebrans fundamentalsats har en n-tegrads polynomfunktion n stycken nollställen, om man räknar med komplexa nollställen och om man räknar dubbelrötter som 2, trippelrötter som 3 och så vidare. Ditt svar är alltså fel.

Om mitt svar är fel, hur löser man uppgiften annars? 

Maria123 skrev:

Om mitt svar är fel, hur löser man uppgiften annars? 

Man sätter bara en undre begräsning på $n$. Tänk om $n=15$, då har du ekvationen $x^{14}(x-1)=0$. Hur många lösningar har den?

X1= 1 och X2= 0. Alltså 2 lösningar

Maria123 skrev:

X1= 1 och X2= 0. Alltså 2 lösningar

Det är lite här problemet ligger. $x=1$ är en lösning, men sedan har du ekvationen $x^{14}=0$. Där är $x=0$ inte bara en lösning, utan fjorton lösningar. Man säger då att $x=0$ är en rot med multiplicitet 14 (den har alltså 14 identiska rötter).