Oändliga produkter

Hej!

Här kommer två oändliga produkter. Uppgiften är att bestämma deras värden exakt. a)-uppgiften tycker jag är lättare än b), men det kan nog variera litegrann från person till person.

$a)$ $\displaystyle\prod_{k=2}^\infty \frac{k^3-1}{k^3+1}=\dfrac{2^3-1}{2^3+1}\cdot\dfrac{3^3-1}{3^3+1}\cdot...$

$b)$ $\displaystyle\prod_{k=2}^\infty \frac{k^2-1}{k^2+1}=\dfrac{2^2-1}{2^2+1}\cdot\dfrac{3^2-1}{3^2+1}\cdot...$

Visa spoiler

Problemen är ekvivalenta med att bestämma serien

$\displaystyle\sum_{k=2}^\infty \ln (1-\frac{2}{k^p+1})$

för $p=2$ samt $p=3$ .

Albiki skrev:

Visa spoiler

Problemen är ekvivalenta med att bestämma serien

$\displaystyle\sum_{k=2}^\infty \ln (1-\frac{2}{k^p+1})$

för $p=2$ samt $p=3$ .

Intressant observation!

Tack vare logaritmlagarna omvandlas ju produkten till en summa. Hur fortsätter du härifrån?

Visa spoiler

Nästa steg kan vara att skriva seriens partialsumma som

$\displaystyle-\sum_{k=2}^{n}\ln\left(1-\frac{2}{1+k^p}\right) = \sum_{i=2}^{n-1} (i-1)A_{i,i+1}$

där det definierats

$\displaystyle A_{i,j} = \int_{1-2(1+i^p)^{-1}}^{1-2(1+j^p)^{-1}}\frac{1}{t}\,dt\ , \quad 2 \leq i < j \leq n.$

Vilka mattekunskaper måste man ha för att förstå dessa tal? Läser fysik men dessa uppgifter känns inte så bekanta :o

Soderstrom skrev:
Vilka mattekunskaper måste man ha för att förstå dessa tal? Läser fysik men dessa uppgifter känns inte så bekanta :o

Nä, det är inga standarduppgifter, det är sant. Däremot kräver iallafall inte a)-uppgiften särskilt mycket avancerad kunskap, men en del finurlighet. :-)

För den som vill ha en ledtråd på a) kan jag säga följande:

Visa spoiler

Produkten är teleskoperande, det vill säga att en hel del av faktorerna tar ut varandra.

Rolig uppgift, tror jag fick till den till slut! Alltså a). b)-uppgiften känns spontant svårare.

Visa spoiler

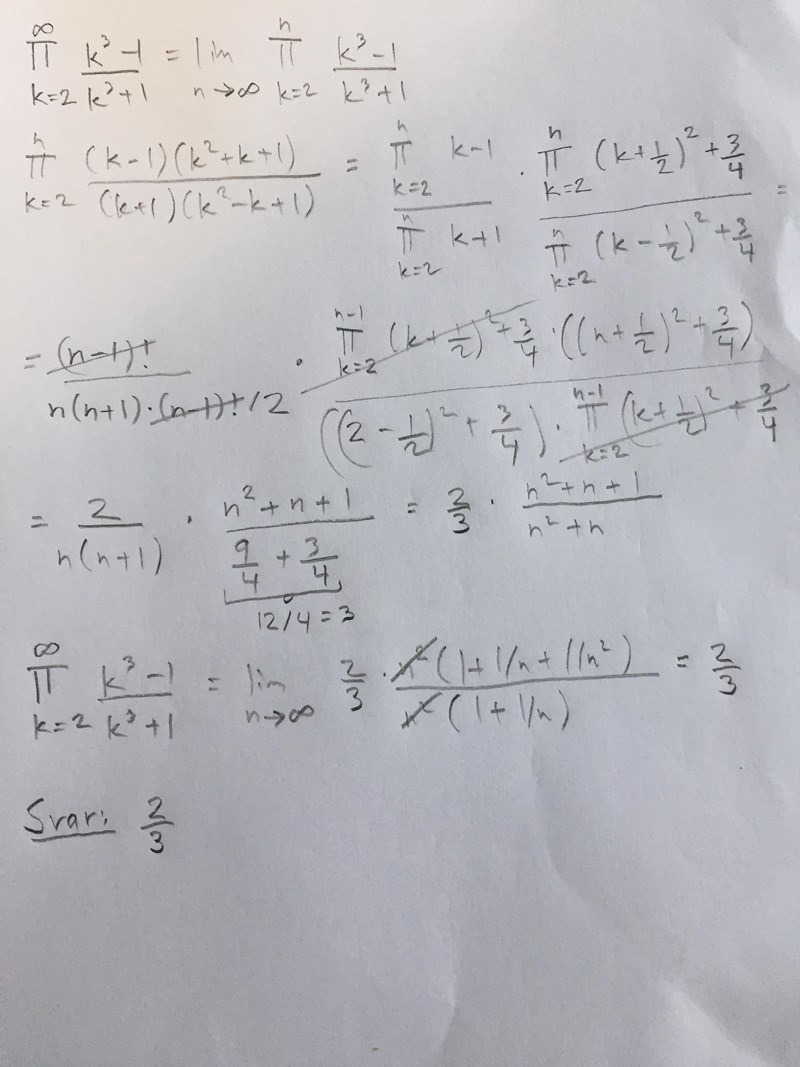Skriv ditt dolda innehåll här

Albiki skrev:

Visa spoiler

Nästa steg kan vara att skriva seriens partialsumma som

$\displaystyle-\sum_{k=2}^{n}\ln\left(1-\frac{2}{1+k^p}\right) = \sum_{i=2}^{n-1} (i-1)A_{i,i+1}$

där det definierats

$\displaystyle A_{i,j} = \int_{1-2(1+i^p)^{-1}}^{1-2(1+j^p)^{-1}}\frac{1}{t}\,dt\ , \quad 2 \leq i < j \leq n.$

Visa spoiler

Noterar att

$\displaystyle\sum_{i=2}^{n-1}A_{i,i+1} = \int_{1-2(1+2^{p})^{-1}}^{1}\frac{1}{t}\,dt = -\ln\left(1-\frac{2}{1+2^{p}}\right)$

så att partialsumman skrivs

$\displaystyle-\sum_{k=2}^{n}\ln\left(1-\frac{2}{1+k^{p}}\right)=\ln \left(1-\frac{2}{1+2^{p}}\right) + \sum_{i=2}^{n-1}i \cdot A_{i,i+1}.$

Tror även jag fick till b) nu medelst...

Visa spoiler

Weierstrass och gränsvärden.

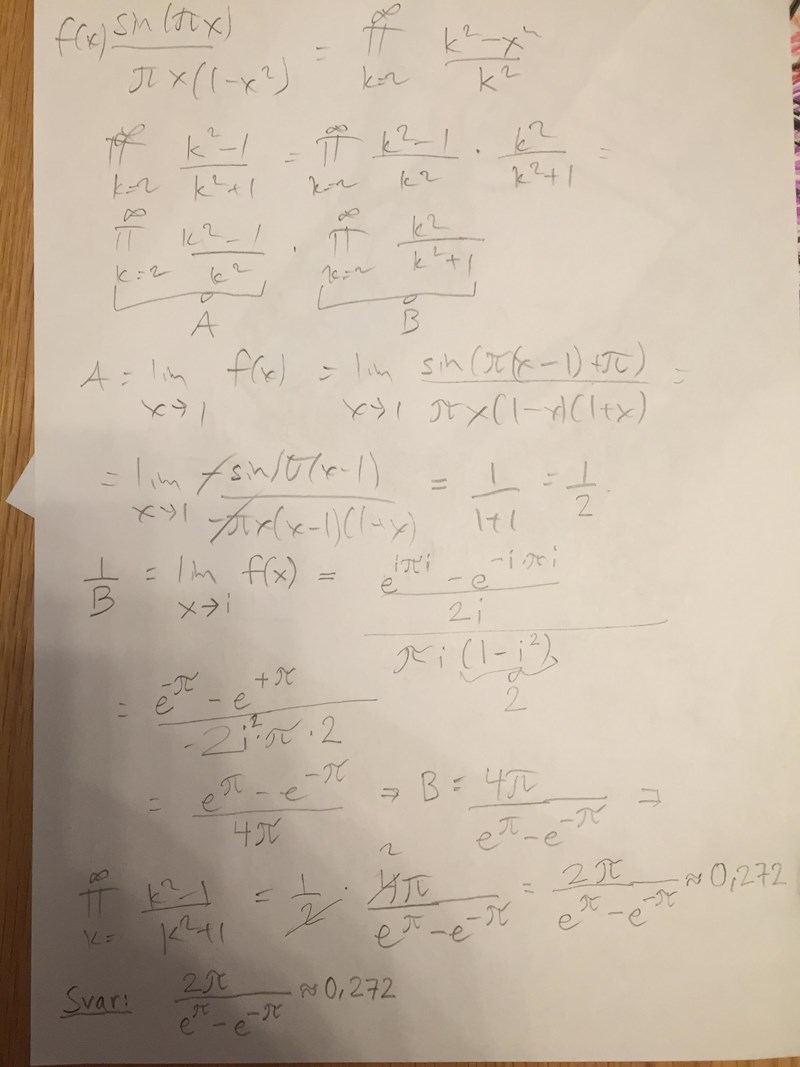
@AlvinB, var det dessa lösningar du gjort också? Eller löste du dem på något annat sätt?

tomast, mycket eleganta lösningar på båda problem!

Jag hade väsentligen samma lösningsidéer, men jag måste säga att du presenterade dem snyggare än jag. På den första måste jag säga att det var ett smart trick att dela upp det hela i flera produkter. Min egen framställning av samma idé blev något rörig när jag försökte beskriva det hela utan att dela upp i flera produkter.

På den andra använde jag också mig av produkter som härstammar ur Weierstraß faktorsats, även om jag också utnyttjade produkten för $\sinh(x)$ (som ju är lika med $\sin(ix)$ ). Din och min framställning är ju i grunden samma, men skiljer sig så till vida att din framställning enbart kräver sinusprodukten, medan min kräver både sinusprodukten och hyperbolisk-sinus-produkten. Å andra sidan kan man undvika komplexa tal helt och hållet med $\sin(x)$ och $\sinh(x)$ , vilket kan vara fördelaktigt eftersom dessa produkter kan bevisas relativt enkelt för reella $x$ (se t.ex. här) medan beviset för komplexa $x$ är mer invecklat.

Albiki verkar också ha något spännande på gång. Kanske är det möjligt med en sådan metod att beräkna båda produkter i ett svep? I sådana fall blir jag mycket imponerad.

Jag tyckte problemet var intressant eftersom de två produkterna ger så helt olika svar och de lösningsgångar jag hittade var helt olika. Lite spännande är det också att undersöka vad som händer för andra exponenter, säg $4$ :

$\displaystyle\prod_{k=2}^\infty \frac{k^4-1}{k^4+1}$

Denna produkt ökar svårighetsgraden ytterligare. Denna kan den som orkar få som en c)-uppgift. :-)
För exponenten $5$ har jag över huvud tagit inte lyckats lösa problemet. Ingen av metoderna jag har kommit på verkar gå att generalisera.

Svara Avbryt

Visa senaste svar